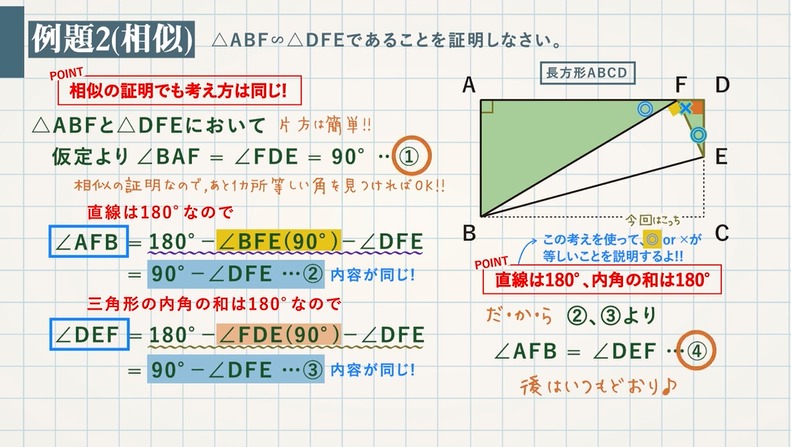
出題範囲は違う(直角三角形」と「相似」)けど、ポイント・考え方はまったく同じ問題があります。

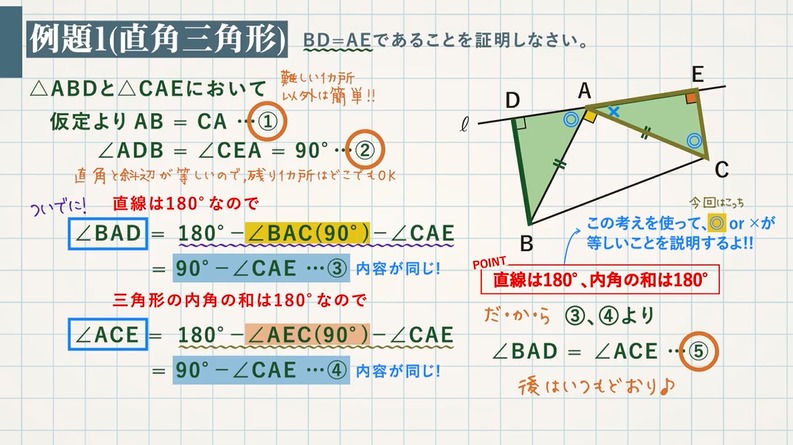
【例題 $\textcolor{green}{1}$ (直角三角形)】$\textcolor{green}{\rm BD = AE}$ であることを証明しなさい。

$\rm △ABD$ と $\rm △CACE$ において、

仮定より $\textcolor{blue}{\rm AB=CA}…①$ 

$\textcolor{blue}{\rm ∠ADB=∠CEA=90°}…②$

(直角と斜辺が等しいので、残り $1$ カ所はどこでもOK)

POINT：直線は $\textcolor{blue}{180°}$、内角の和は $\textcolor{blue}{180°}$

直線は $180°$ なので、

$\rm ∠BAD=180°-∠BAC(90°)-∠CAE$

　　　   $=\textcolor{blue}{\rm 90°-∠CAE}…③$

三角形の内角の和は $180°$ なので

$\rm ∠ACE=180°-∠AEC(90°)-∠CAE$

　　 　  $=\textcolor{blue}{\rm 90°-∠CAE}…④$

③,④より　$\textcolor{blue}{\rm ∠BAD=∠ACE}$…⑤

①,②,⑤より、斜辺と $1$ つの鋭角がそれぞれ等しいので、$\textcolor{blue}{\rm △ABD≡△CAE}$

合同な図形の対応する辺の長さは等しいので、$\textcolor{blue}{\rm BD=AE}$ である。

相似の問題でも考え方は同じになります。

【例題 $\textcolor{green}{2}$ (相似)】$\textcolor{green}{\rm △ABF∽△DFE}$  であることを証明しなさい。

$\rm △ABF$ と $\rm △DFE$ において

仮定より $\textcolor{blue}{\rm ∠BAF=∠FDE=90°}$…①

相似の証明なので、あと $1$ カ所等しい角を見つければOK！

直線は $180°$ なので

$\rm ∠AFB=180°-∠BFE(90°)-∠DFE$

　　　  $=\textcolor{blue}{\rm 90°-∠DFE}$…②

三角形の内角の和は $180°$ なので

$\rm ∠DEF=180°-∠FDE(90°)-∠DFE$

　　　  $\textcolor{blue}{\rm =90°-∠DFE}$…③

②,③より

$\textcolor{blue}{\rm ∠AFB=∠DEF}$…④

①,④より　$2$ 組の角がそれぞれ等しいので

$\textcolor{blue}{\rm △ABF∽△DFE}$