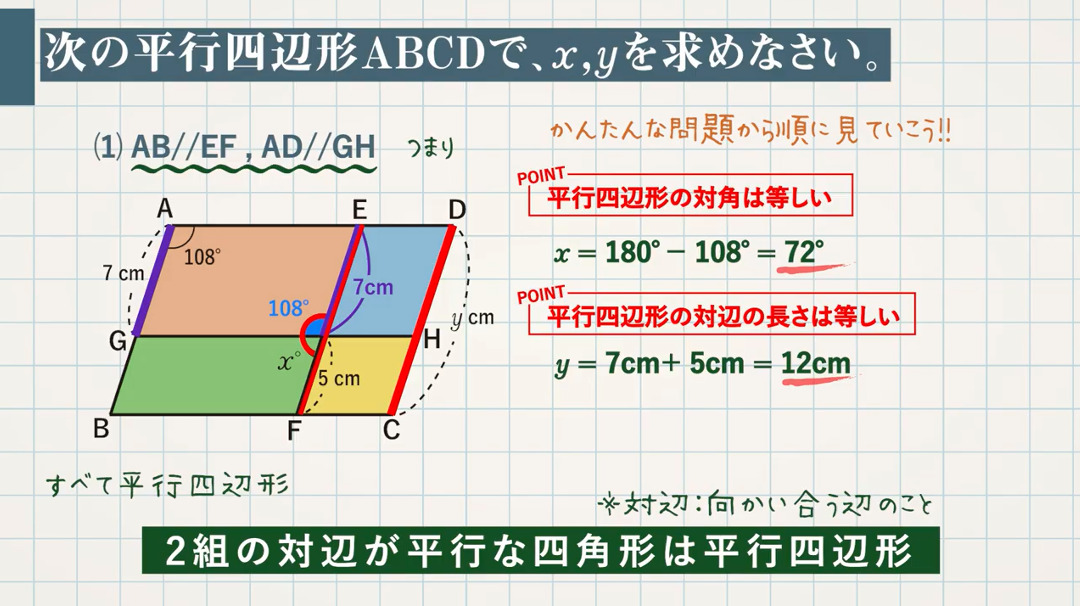
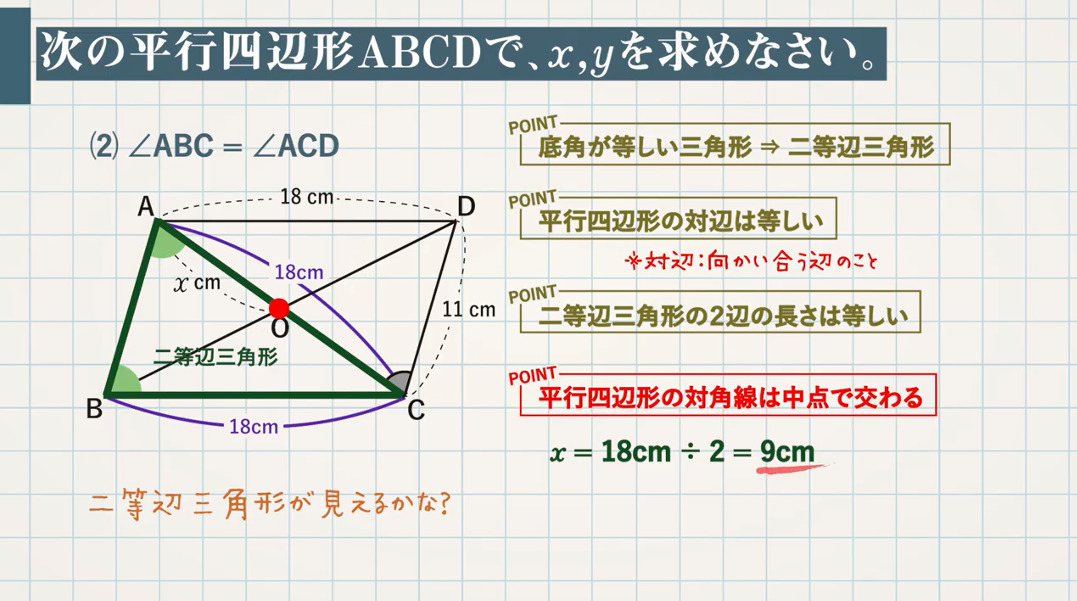
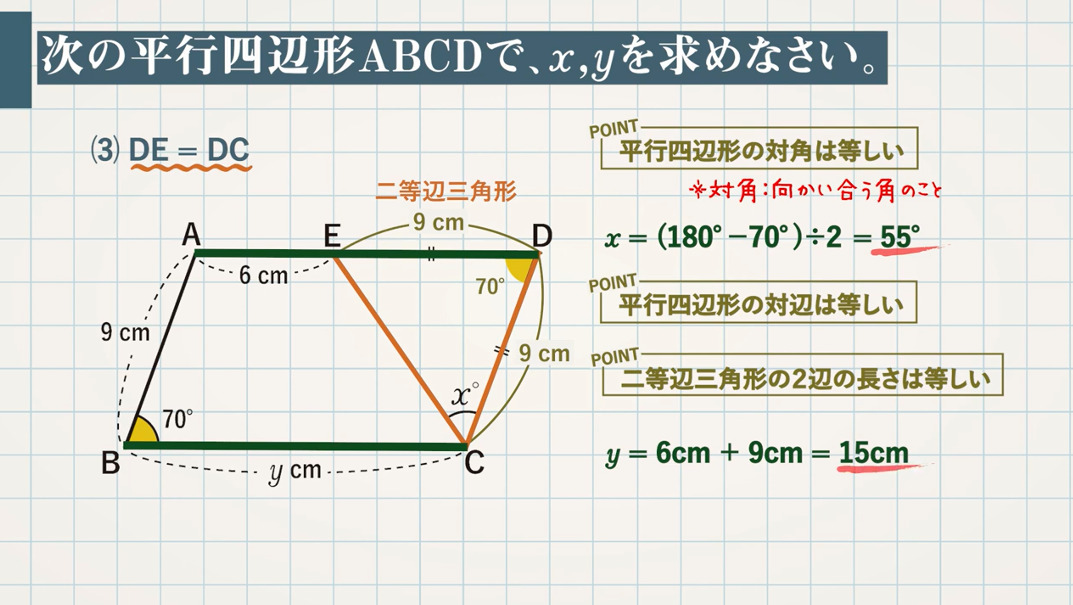
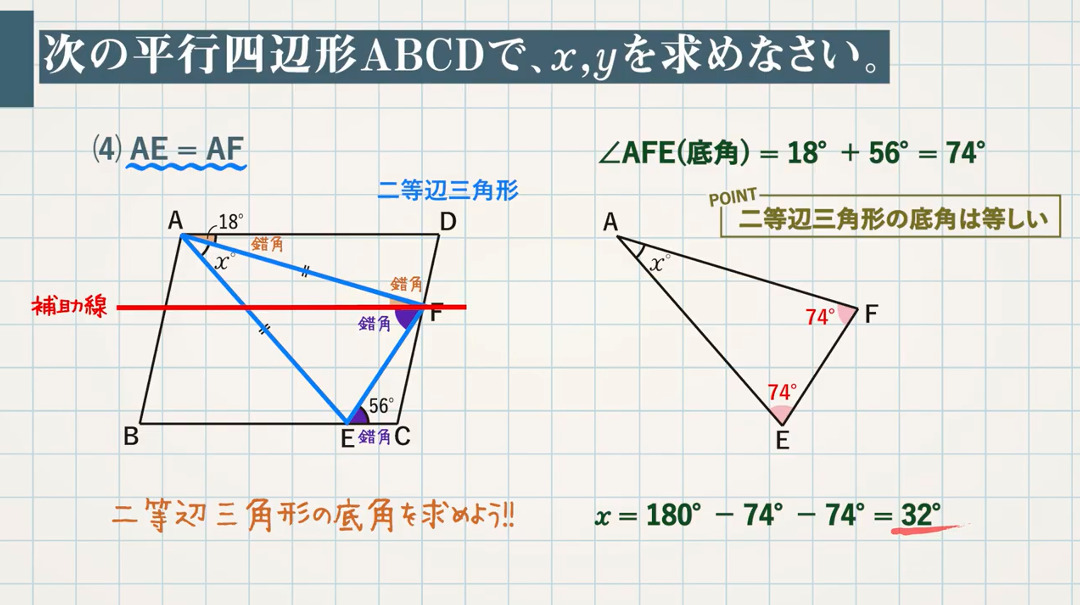
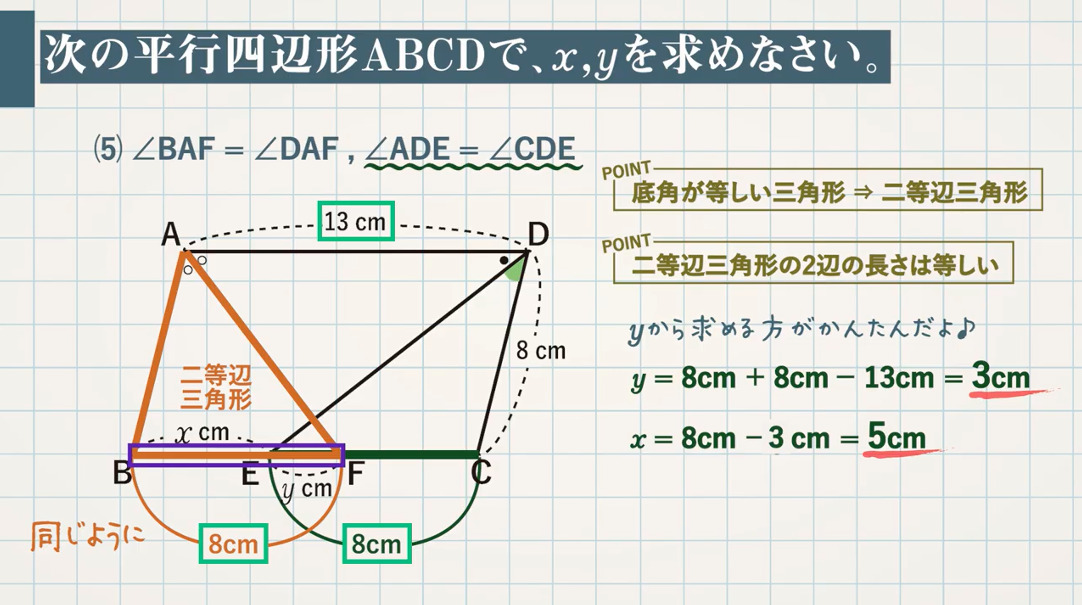
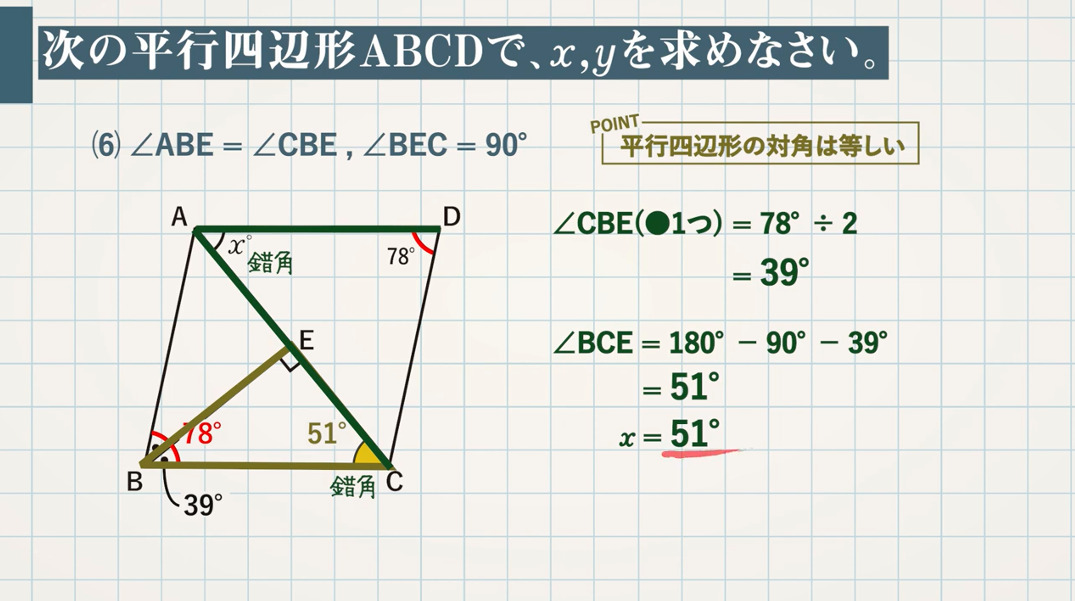
次の平行四辺形 $\textcolor{green}{\rm ABCD}$ で、$\textcolor{green}{x,y}$ を求めなさい。

(1) $\textcolor{green}{\rm AB//EF , AD//GH}$

→つまり、$4$ 色の四角形は、すべて平行四辺形

POINT：平行四辺形の対角は等しい

$x=180°-108°=\textcolor{red}{72°}$

POINT：平行四辺形の対辺の長さは等しい

$y=7\rm cm+5cm=\textcolor{red}{12cm}$

(2) $\textcolor{green}{\rm ∠ABC=∠ACD}$

平行線の錯角は等しいので、$\rm ∠BAC=∠ACD$

よって、$\rm ∠ABC=∠BAC$ となることから、$\rm △ABC$ は $\rm AB$ を底辺とした二等辺三角形であることがわかります。

POINT：底角が等しい三角形→二等辺三角形

POINT：平行四辺形の対辺は等しい

$\rm AD=BC=18cm$

POINT：二等辺三角形の $\textcolor{blue}{2}$ 辺の長さは等しい

$\rm BC=AC=18cm$

POINT：平行四辺形の対角線は中点で交わる

$x=\rm 18cm÷2=\textcolor{red}{9cm}$

(3) $\textcolor{green}{\rm DE=DC}$

POINT：平行四辺形の対角は等しい

$\rm ∠ABC=∠CDE=70°$

$\rm △CDE$ は $\rm DE=DC$ の二等辺三角形なので、その底角は等しい。

よって、$x=(180°-70°)÷2=\textcolor{red}{55°}$

POINT：平行四辺形の対辺は等しい

$\rm AB=DC=9cm$

POINT：二等辺三角形の $\textcolor{blue}{2}$ 辺の長さは等しい

$\rm DE=DC=9cm$

POINT：平行四辺形の対辺は等しい

$y\rm =6cm+9cm=\textcolor{red}{15cm}$

(4) $\textcolor{green}{\rm AE=AF}$

$\rm AE=AF$ より、$\rm △AEF$は二等辺三角形。二等辺三角形の底角を求めましょう。

補助線をひくと、$\rm ∠AFE$（底角）は $2$ つの錯角の合計なので、$18°+56°=\textcolor{blue}{74°}$

POINT：二等辺三角形の底角は等しい

$x=180°-74°-74°=\textcolor{red}{32°}$

(5) $\textcolor{green}{\rm ∠BAF=∠DAF,∠ADE=∠CDE}$

平行線の錯角は等しいので、$\rm ∠ADE=∠CED$

$\rm ∠ADE=∠CDE$ より、$\rm ∠CED=∠CDE$

POINT：底角が等しい三角形→二等辺三角形

POINT：二等辺三角形の $\textcolor{blue}{2}$ 辺の長さは等しい

$\rm DC=EC=8cm$

同じように、$\rm △ABF$ も二等辺三角形であるため、

$\rm AB=BF=8cm$

よって、$y=\rm 8cm+8cm-13cm=\textcolor{red}{3cm}$

$x=\rm 8cm-$$y\rm cm=\rm 8cm-3cm=\textcolor{red}{5cm}$

(6) $\textcolor{green}{\rm ∠ABE=∠CBE,∠BEC=90°}$

POINT：平行四辺形の対角は等しい

$\rm ∠D=∠B=78°$

$\rm ∠CBE$（●1つ）$=78°÷2=39°$

三角形の内角の和は $180°$ なので、

$\rm ∠BCE=180°-90°-39°=51°$

平行線の錯角は等しいので、

$\rm ∠BCE=∠DAC$  よって、$x=\textcolor{red}{51°}$