PDF教材

ダウンロード

二等辺三角形について、まずは定義と定理・性質の確認をしましょう。

（定理）$\textcolor{blue}{2}$ 辺が等しい三角形

底辺の両端の角を底角、てっぺんの角を頂角といいます。

（定理・性質）

$\textcolor{blue}{1}$：$\textcolor{blue}{2}$ つの底角は愛しい

$\textcolor{blue}{2}$：頂角の二等分線は、底辺を垂直に二等分する

二等辺三角形になるための条件（定義と定理を使う）

・$\textcolor{blue}{2}$ 辺が等しい　・$\textcolor{blue}{2}$ つの角(底角)が等しい

このどちらかを証明できれば、二等辺三角形だと言えます。

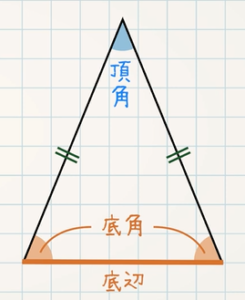
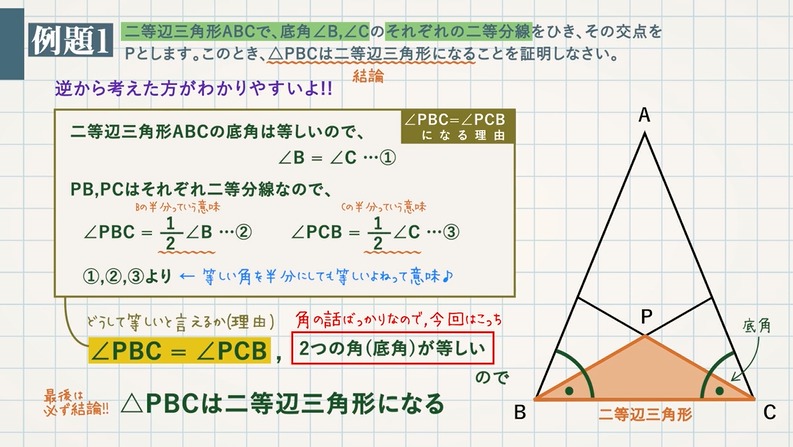
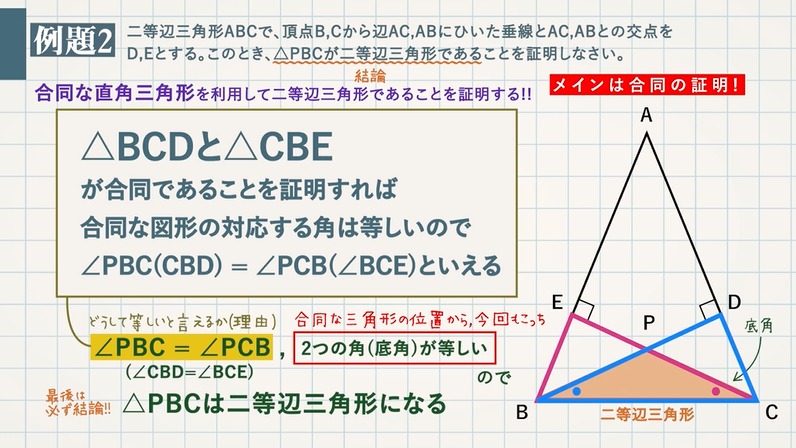
【例題 $\textcolor{green}{1}$ 】二等辺三角形 $\textcolor{green}{\rm ABC}$ で、底角 $\textcolor{green}{\rm ∠B,∠C}$ のそれぞれの二等分線をひき、その交点を $\textcolor{green}{\rm P}$ とします。このとき、$\textcolor{green}{\rm △PBC}$ は二等辺三角形になることを証明しなさい。

※逆から考えた方がわかりやすいです。

最後は必ず結論なので、「$\textcolor{blue}{\rm △PBC}$ は二等辺三角形になる」

二等辺三角形といえるためには、

$\textcolor{blue}{2}$ 辺が等しい　or　$\textcolor{blue}{2}$ つの角(底角)が等しい

角の話ばかりなので、今回は$\textcolor{blue}{2}$ つの角(底角)が等しいので

→ $\textcolor{blue}{\rm ∠PBC=∠PCB}$

どうして $\textcolor{blue}{\rm ∠PBC=∠PCB}$ といえるのか理由を説明

二等辺三角形 $\rm ABC$ の底角は等しいので、$\textcolor{blue}{\rm ∠B=∠C…①}$

$\rm PB,PC$ はそれぞれ二等分線なので、

$\textcolor{blue}{\rm ∠PBC=\frac{1}{2}B…②}$　$\textcolor{blue}{\rm ∠PCB=\frac{1}{2}C…③}$

①,②,③より

この流れを逆に書いていけば、証明が完成します。(画像の緑文字部分)

【例題 $\textcolor{green}{2}$ 】二等辺三角形 $\textcolor{green}{\rm ABC}$ で、頂点 $\textcolor{green}{\rm B,C}$ から辺 $\textcolor{green}{\rm AC,AB}$ にひいた垂線と $\textcolor{green}{\rm AC,AB}$ との交点を $\textcolor{green}{\rm D,E}$ とする。このとき、$\textcolor{green}{\rm △PBC}$ が二等辺線三角形であることを証明しなさい。

この問題は、合同な直角三角形を利用して二等辺三角形であることを証明します。先ほどと同じように逆から考えると、

結論「$\textcolor{blue}{\rm △PBC}$ は二等辺三角形になる」

二等辺三角形といえるためには、

$\textcolor{blue}{2}$ 辺が等しい　or　$\textcolor{blue}{2}$ つの角(底角)が等しい

合同な三角形の位置から、今回も$\textcolor{blue}{2}$ つの角(底角)が等しいので

→ $\textcolor{blue}{\rm ∠PBC=∠PCB}$

どうして $\textcolor{blue}{\rm ∠PBC=∠PCB}$ といえるのか理由を説明

$\textcolor{blue}{\rm △BCD}$ (水色) と $\textcolor{blue}{\rm △CBE}$ (ピンク) が合同であることを証明すれば、合同な図形の対応する角は等しいので、$\textcolor{blue}{\rm ∠PBC(CBD)=∠PCB(∠BCE)}$ といえる。