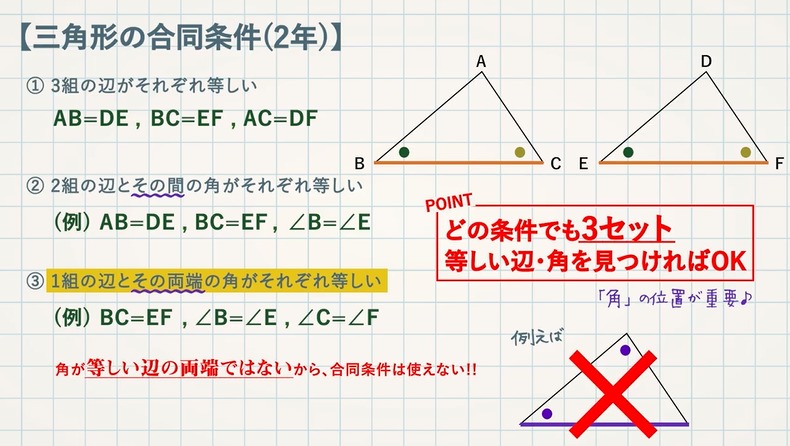
何かと嫌がられる証明問題ですが、書き方（流れ）を覚えると、効率の良い得点源になります。

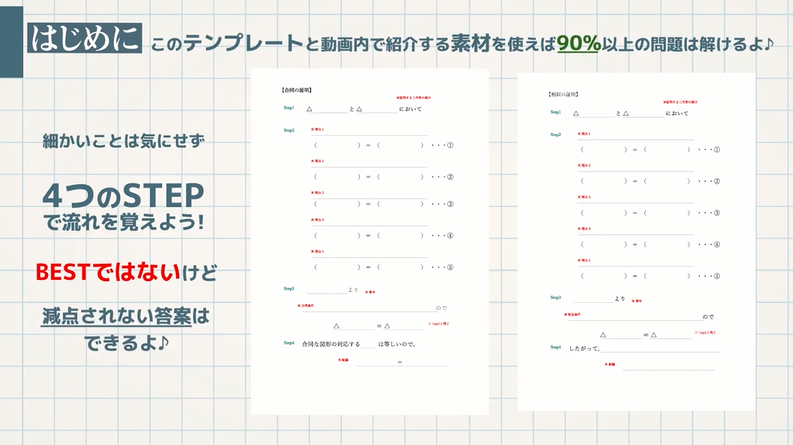
上にあるテンプレート（解答用紙）と動画内で紹介する素材を使えば $\textcolor{blue}{90}$ %以上の証明問題は解けます。証明問題は計算ミスもなく、簡単な問題でも配点が大きいものとなるので、しっかり確認しましょう。

 $\textcolor{blue}{4}$ つのSTEPで証明問題を解くための流れを覚えましょう。BESTではないけど、減点されない答案は作ることができます。

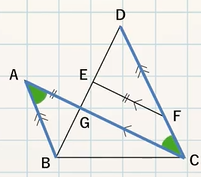
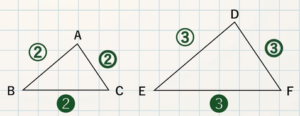
STEP $\textcolor{blue}{1}$ ：$\textcolor{blue}{2}$ つの三角形の紹介 

　$\textcolor{blue}{↓}$

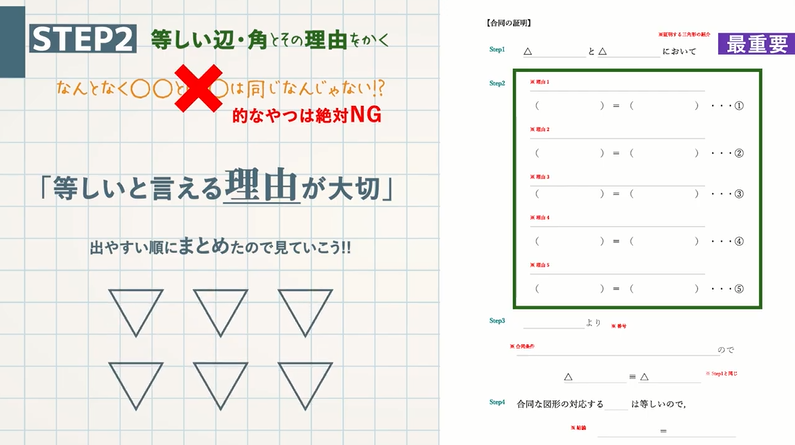
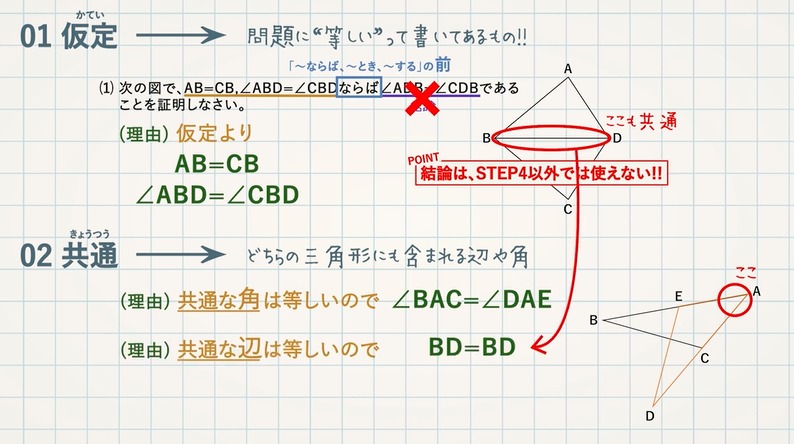
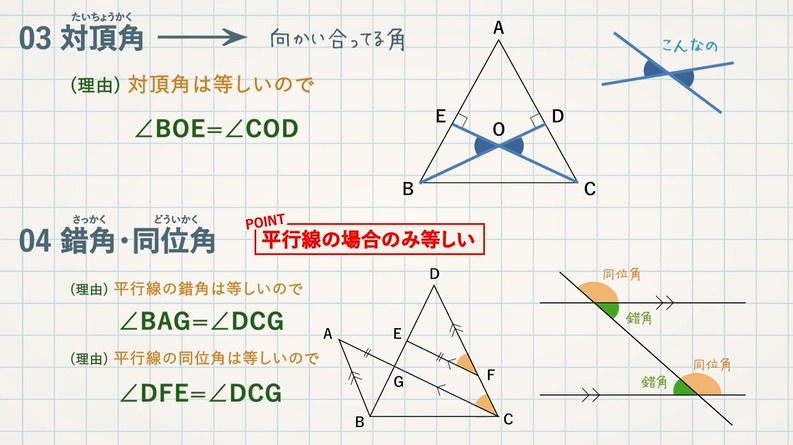
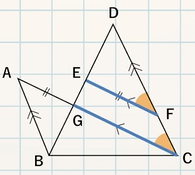
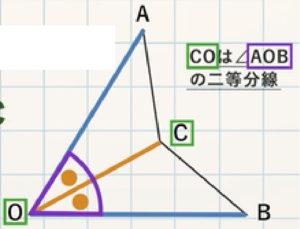
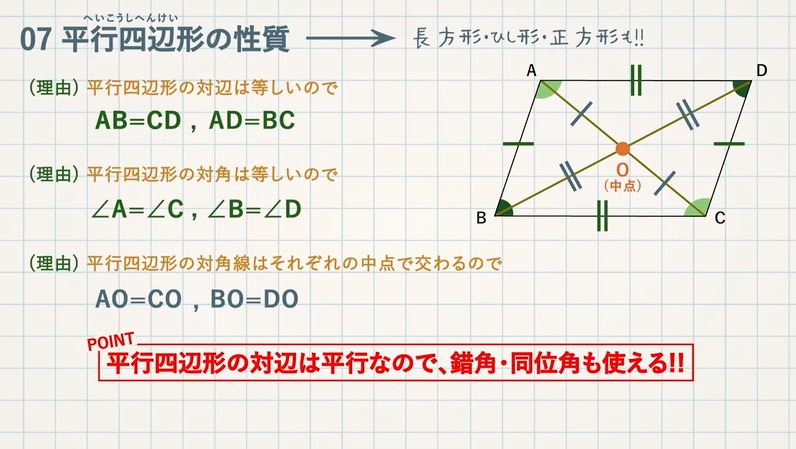
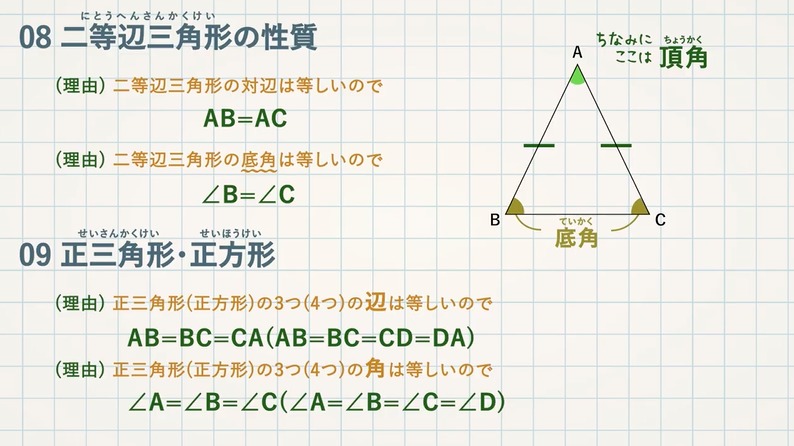
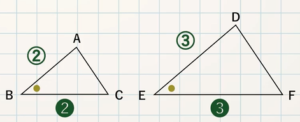
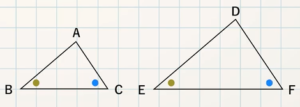
STEP $\textcolor{blue}{2}$ ：等しい辺・角とその理由をかく

　$\textcolor{blue}{↓}$

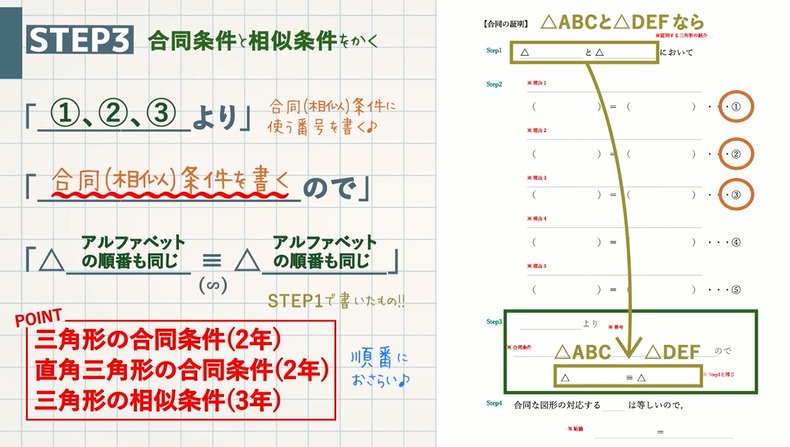
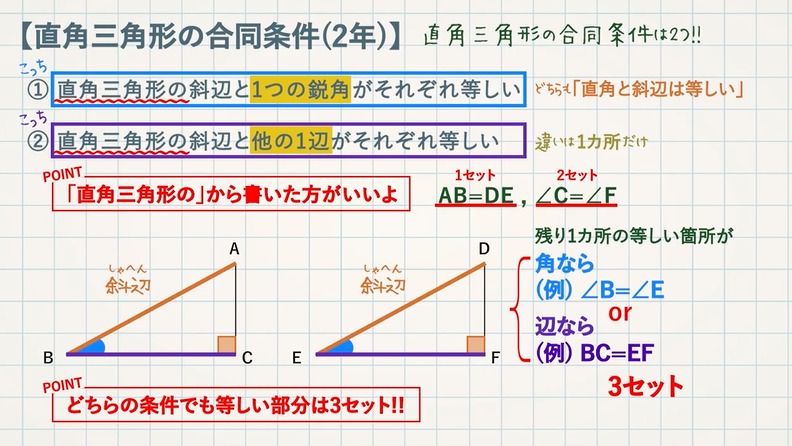
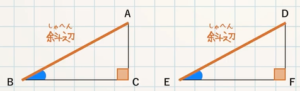
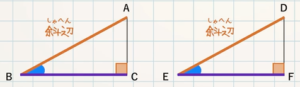
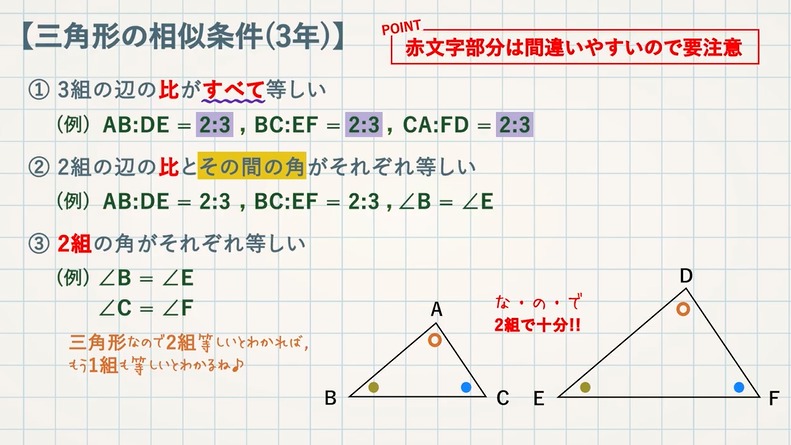
STEP $\textcolor{blue}{3}$ ：合同条件と相似条件をかく

　$\textcolor{blue}{↓}$

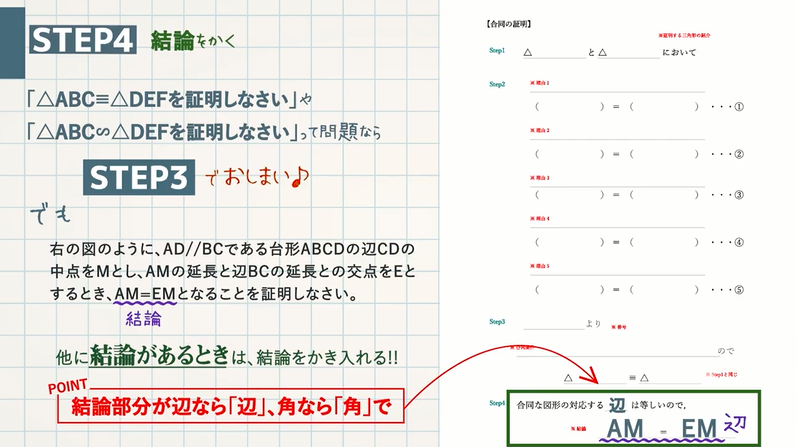
STEP $\textcolor{blue}{4}$ ：結論をかく

証明のはじまりは、$2$ つの三角形の紹介になります。

仮定　$\rm AB=DC$ , $\rm ∠ABC=∠DCB$

結論　$\rm ∠A=∠D$　　

POINT：仮定と結論が含まれた三角形を選ぶ

POINT：$\textcolor{blue}{2}$ つ目の三角形をかくときは頂点をそろえる

仮定と結論より、

$\textcolor{blue}{\rm A}$ に対応する頂点　→　$\textcolor{blue}{\rm D}$

$\textcolor{blue}{\rm B}$ に対応する頂点　→　$\textcolor{blue}{\rm C}$

$\textcolor{blue}{\rm C}$ に対応する頂点　→　$\textcolor{blue}{\rm B}$

よって、$2$ つの三角形は $\textcolor{blue}{\rm △ABC}$と$\textcolor{blue}{\rm △DCB}$ 。証明のはじまりは「$\textcolor{blue}{\rm △ABC}$ と $\textcolor{blue}{\rm △DCB}$ において」となります。

続いて、$\textcolor{blue}{2}$ つの三角形の等しい辺・角とその理由をかきます

最重要となるSTEPです。なんとなく見た目で〇〇と〇〇は同じなんじゃない？的なやつな絶対にNGです。

ここでは、「等しいと言える理由が大切」になります。

出やすい順にまとめたので、見ていきましょう。

$\textcolor{blue}{01}$ 仮定　→　問題に“等しい”と書いてあるもの

【例題】次の図で、$\rm AB=CD$、$\rm ∠ABD=∠CBD$ ならば、$\rm ∠ADB=∠CDB$ であることを証明しなさい。

であれば、仮定は次のようになります。

(理由) 仮定より、$\textcolor{blue}{\rm AB=CD}$　$\textcolor{blue}{\rm ∠ABD=∠CBD}$

※問題文には、$\rm ∠ADB=∠CDB$ もありますが、これは結論になります。結論はSTEP $\textcolor{blue}
{4}$  以外では使えません。

「～ならば、～とき、～する」の前が仮定になると覚えましょう。

$\textcolor{blue}{02}$ 共通　→　どちらの三角形にも含まれる辺や角 (図参照)

(理由)　共通な角は等しいので、$\textcolor{blue}{\rm ∠BAC=∠DAE}$

(理由)　共通な辺は等しいので、$\textcolor{blue}{\rm BD=BD}$

$\textcolor{blue}{03}$ 対頂角　→　向かい合ってる角 (図参照)

(理由) 対頂角は等しいので、$\textcolor{blue}{\rm ∠BOE=∠COD}$

$\textcolor{blue}{04}$ 錯角・同位角　→　POINT ：平行線の場合のみ等しい

(理由) 平行線の錯角は等しいので、$\textcolor{blue}{\rm ∠BAG=∠DCG}$

(理由) 平行線の同位角は等しいので、$\textcolor{blue}{\rm ∠DFE=∠DCG}$

$\textcolor{blue}{05}$ 中点　→　両端から等しい位置(真ん中)にある点

(理由) 点$\textcolor{blue}{\rm M}$ は辺 $\textcolor{blue}{\rm CD}$ の中点なので、$\textcolor{blue}{\rm DM=CM}$

$\textcolor{blue}{06}$ 角の二等分線　→　角を二等分する線

(理由) 辺 $\textcolor{blue}{\rm CO}$ は $\textcolor{blue}{\rm ∠AOB}$ の二等分線なので、

$\textcolor{blue}{\rm ∠AOC=∠BOC}$

$\textcolor{blue}{07}$ 平行四辺形の性質　→　長方形・ひし形・正方形もあてはまります。 (図参照)　

(理由) 平行四辺形の対辺は等しいので、

　　　$\textcolor{blue}{\rm AB=CD}$ , $\textcolor{blue}{\rm AD=BC}$

(理由) 平行四辺形の対角は等しいので、

　　　$\textcolor{blue}{\rm ∠A=∠C}$ , $\textcolor{blue}{\rm ∠B=∠D}$

(理由) 平行四辺形の対角線はそれぞれの中点で交わるので、

　　　$\textcolor{blue}{\rm AO=CO}$ , $\textcolor{blue}{\rm BO=DO}$

このほか、平行四辺形の対辺は平行なので、錯角・同位角も使えます。

$\textcolor{blue}{08}$ 二等辺三角形の性質　→　底辺の両端の角を底角、等しい$\textcolor{blue}{2}$ 辺のつくる角を頂角といいます。 (図参照)　

(理由) 二等辺三角形の対辺は等しいので、$\textcolor{blue}{\rm AB=AC}$

(理由) 二等辺三角形の底角は等しいので、$\textcolor{blue}{\rm ∠B=∠C}$

$\textcolor{blue}{09}$ 正三角形・正方形

(理由) 正三角形(正方形)の$\textcolor{blue}{3}$ つ( $\textcolor{blue}{4}$ つ)の辺は等しいので、

$\textcolor{blue}{\rm AB=BC=CA（AB=BC=CD=DA）}$

(理由) 正三角形(正方形)の$\textcolor{blue}{3}$ つ( $\textcolor{blue}{4}$ つ)の角は等しいので、

$\textcolor{blue}{\rm ∠A=∠B=∠C（∠A=∠B=∠C=∠D）}$

$\textcolor{blue}{10}$ 辺の比が等しい　→　BESTではないけど、このテンプレートを使う場合 (図参照)　

$\rm △ABD$ と $\rm △DBC$ において、

(理由) $\textcolor{blue}{\rm AB=9cm}$ , $\textcolor{blue}{\rm DB=12cm}$ より、

　　　$\textcolor{blue}{\rm AB:DB=3:4}・・・①$

(理由) $\textcolor{blue}{\rm BD=12cm}$ , $\textcolor{blue}{\rm BC=16cm}$ より、

　　　$\textcolor{blue}{\rm BD:BC=3:4}・・・②$

(理由) $\textcolor{blue}{\rm DA=6cm}$ , $\textcolor{blue}{\rm CD=8cm}$ より、

　　　$\textcolor{blue}{\rm DA:CD=3:4}・・・③$

POINT：ここはテンプレートに合わせなくてもOK！慣れた書き方で！！

等しい辺や角を理由とともに説明したら、合同条件・相似条件をかきます。

「①,②,③ より」 →合同(相似)条件に使う番号を書きます。

「 合同(相似)条件を書く ので」

「△〇〇〇≡(∽) △〇〇〇」　

→STEP $\textcolor{blue}{1}$ の $\textcolor{blue}{2}$ つの三角形と同じアルファベットの順番で

POINT：三角形の合同条件($\textcolor{blue}{2}$年)、直角三角形の合同条件($\textcolor{blue}{2}$年)、三角形の相似条件($\textcolor{blue}{3}$年) を順番におさらいしましょう。

【三角形の合同条件( $2$ 年)】

① $\textcolor{blue}{3}$ 組の辺がそれぞれ等しい

　$\textcolor{blue}{\rm AB=DE}$ , $\textcolor{blue}{\rm BC=EF}$ , $\textcolor{blue}{\rm AC=DF}$

② $\textcolor{blue}{2}$ 組の辺とその間の角がそれぞれ等しい

(例) $\textcolor{blue}{\rm AB=DE}$ , $\textcolor{blue}{\rm BC=EF}$ , $\textcolor{blue}{\rm ∠B=∠E}$

③ $\textcolor{blue}{1}$ 組の辺とその両端の角がそれぞれ等しい

(例) $\textcolor{blue}{\rm BC=EF}$ , $\textcolor{blue}{\rm ∠B=∠E}$ , $\textcolor{blue}{\rm ∠C=∠F}$

POINT：どの条件でも $\textcolor{blue}{3}$ セット等しい辺・角を見つければOK　※「角」の位置が重要

【直角三角形の合同条件】

① 直角三角形の斜辺と $\textcolor{blue}{1}$ つの鋭角がそれぞれ等しい

② 直角三角形の斜辺と他の $\textcolor{blue}{1}$ 辺がそれぞれ等しい 

どちらの条件も「直角と斜辺は等しい」ので、違いは $1$ カ所だけになります。

残り $1$ カ所の等しい箇所が「角」なら、(例) $\textcolor{blue}{\rm ∠B=∠E}$ 

→ ① 直角三角形の斜辺と $\textcolor{blue}{1}$ つの鋭角がそれぞれ等しい

残り $1$ カ所の等しい箇所が「辺」なら、(例) $\textcolor{blue}{\rm BC=EF}$ 

→ ② 直角三角形の斜辺と他の $\textcolor{blue}{1}$ 辺がそれぞれ等しい 

POINT：どちらの条件でも等しい部分は $\textcolor{blue}{3}$ セットになります。

【三角形の相似条件( $3$ 年)】

① $\textcolor{blue}{3}$ 組の辺の比がすべて等しい

(例) $\textcolor{blue}{\rm AB:DE=2:3}$ , $\textcolor{blue}{\rm BC:EF=2:3}$ , $\textcolor{blue}{\rm CA:FD=2:3}$

② $\textcolor{blue}{2}$ 組の辺の比とその間の角がそれぞれ等しい

(例) $\textcolor{blue}{\rm AB:DE=2:3}$ , $\textcolor{blue}{\rm BC:EF=2:3}$ , $\textcolor{blue}{\rm  ∠B=∠E}$

③ $\textcolor{blue}{2}$ 組の角がそれぞれ等しい

(例) $\textcolor{blue}{\rm ∠B=∠E}$ , $\textcolor{blue}{\rm  ∠C=∠F}$

最後は結論をかき入れます。

「$\rm △ABC≡△DEF$ を証明しなさい」や　

「$\rm △ABC∽△DEF$ を証明しなさい」という問題なら

STEP $\textcolor{blue}{3}$ で解答はおしまいです。

ただし、次のような問題(他に結論がある)のときは、結論をかき入れます。

【例題】右の図のように、$\rm AD//BC$ である台形 $\rm ABCD$ の辺 $\rm CD$ の中点を $\rm M$ とし、$\rm AM$ の延長と辺 $\rm BC$ の延長との交点を $\rm E$ とするとき、$\textcolor{blue}{\rm AM=EM}$ となることを証明しなさい。 

POINT：結論部分が辺なら「辺」、角なら「角」で

例題は、$\textcolor{blue}{\rm AM=EM}$ なので「辺」をかき入れる

よって結論部分は、「合同な図形の対応する辺は等しいので、$\textcolor{blue}{\rm AM=EM}$」となります。

相似( $\textcolor{blue}{3}$ 年) の場合

「相似な図形の対応する辺の比は等しいので」とか「相似な図形の対応する角は等しいので」→  結論 となります。