\begin{eqnarray}\textcolor{blue}{確率({\rm P})=\frac{〇〇が起こる場合(a)}{起こるすべての場合(n)}}\end{eqnarray}

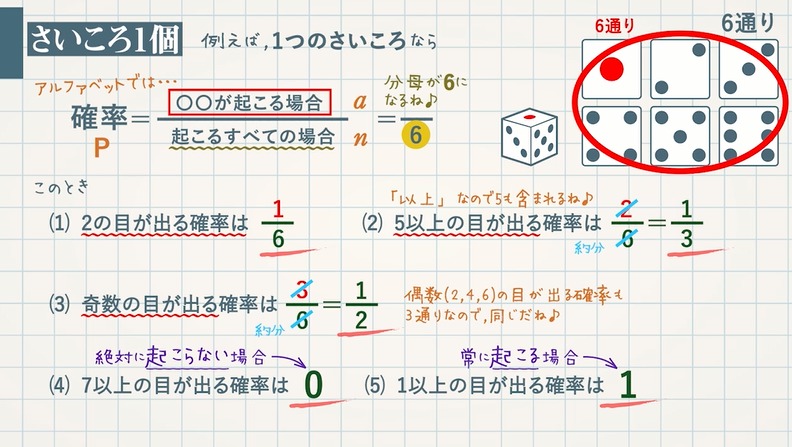
例えば、 $1$ つのさいころなら出る目は $1$~$6$ の $6$ 通りなので、分母が $6$ になります。

(1) $\textcolor{green}{2}$ の目が出る確率　$\textcolor{blue}{1}$ 通りなので、$\textcolor{red}{\frac{1}{6}}$

(2) $\textcolor{green}{5}$ 以上の目が出る確率は　「以上」は $5$ も含まれます。

$\textcolor{blue}{2}$ 通りなので、$\frac{2}{6}=\textcolor{red}{\frac{1}{3}}$

(3) 奇数の目が出る確率は　

$1,3,5$ の $\textcolor{blue}{3}$ 通りなので、$\frac{3}{6}=\textcolor{red}{\frac{1}{3}}$

(4) $\textcolor{green}{7}$ 以上の目が出る確率　絶対に起こらない場合

$\textcolor{blue}{0}$ 通りなので、$\frac{0}{6}=\textcolor{red}{0}$

(5) $\textcolor{green}{1}$ 以上の目が出る確率　常に起こる場合

$\textcolor{blue}{6}$ 通りなので、$\frac{6}{6}=\textcolor{red}{1}$

さいころ $2$ つの場合は, 表を使うとわかりやすいです。

組合せは $6×6$ で $\textcolor{blue}{36}$ 通り

(1) 出る目の和が $\textcolor{green}{7}$ になる確率　$\frac{6}{36}=\textcolor{red}{\frac{1}{6}}$

POINT：和の、ななめラインは同じになる（左図）

(2) 少なくとも一方は $\textcolor{green}{4}$ の目になる確率　$\textcolor{red}{\frac{11}{36}}$

$4$ と $4$ の組み合わせは $2$ 回数えないように注意。（右図）

(3) 出る目の積が奇数になる確率　$\textcolor{red}{\frac{1}{4}}$

POINT：積が奇数になるのは、(奇数 $×$ 奇数) のときだけ

(偶数 $×$ 偶数) 、(偶数 $×$ 奇数) 、(奇数 $×$ 偶数) 、(奇数 $×$ 奇数) $4$ 通りのうちの $\textcolor{blue}{1}$ 通り→ $\textcolor{red}{\frac{1}{4}}$

$\textcolor{green}{2}$ つのさいころを投げ、出た目の数の和と同じ数だけ、石を矢印の向きに動かす。

(1) 石がちょうど一周して点 $\textcolor{green}{\rm A}$ にとまる確率は ($4$ 進む)

→出る目の数の和が $\textcolor{blue}{4}$ になる確率は　$\frac{3}{36}=\textcolor{red}{\frac{1}{12}}$

(2) 石が点 $\textcolor{green}{\rm C}$ にとまる確率は

$\textcolor{blue}{1}$ 周目なら $\textcolor{blue}{2}$ 進んだとき　

$\textcolor{blue}{2}$ 周目なら $\textcolor{blue}{6}$ 進んだとき

$\textcolor{blue}{3}$ 周目なら $\textcolor{blue}{10}$ 進んだとき

$\textcolor{blue}{4}$ 周目なら $\textcolor{blue}{14}$ 進んだとき→✕（出た目の数の和の最高は $\textcolor{blue}{12}$ なので）

石が点 $\rm C$ にとまる確率は

→出る目の数の和が $\textcolor{blue}{2}$ か $\textcolor{blue}{6}$ か $\textcolor{blue}{10}$ になるとき。

よって、$\frac{9}{36}=\textcolor{red}{\frac{1}{4}}$

$\textcolor{green}{2}$ つのさいころを投げ、さいころ $\rm \textcolor{green}{A}$ の出た目を $\textcolor{green}{a}$ 、さいころ $\rm \textcolor{green}{B}$ の出た目を $\textcolor{green}{b}$ とする。

(1) 点( $\textcolor{green}{a}$ , $\textcolor{green}{b}$ ) が直線 $\textcolor{green}{y=x}$ 上にある確率は

さいころ $\rm A$ の出た目が $x$ 座標、さいころ $\rm B$ の出た目が $y$ 座標

$y=x$ 上の座標は、

( $1$ , $1$ )、( $2$ , $2$ )、( $3$ , $3$ )、( $4$ , $4$ )、( $5$ , $5$ )、( $6$ , $6$ ) 

よって、$\frac{6}{36}=\textcolor{red}{\frac{1}{6}}$

(2) 点( $\textcolor{green}{a}$ , $\textcolor{green}{b}$ ) が直線 $\textcolor{green}{y=-\frac{1}{3}x+6}$ 上にある確率は

傾き$\textcolor{blue}{-\frac{1}{3}}$ , 切片 $\textcolor{blue}{6}$ の一次関数

POINT：グラフがなければ、$\textcolor{blue}{6}$ までの自然数になる座標を考える。

式の $x$ に $1$ から $6$ を代入 → ( $3$ , $5$ ) と ($6$ , $4$ ) の $2$ カ所

よって、$\frac{2}{36}=\textcolor{red}{\frac{1}{18}}$