まずは、$2$ 次方程式を使って文章題を解く場合の流れを見ておきましょう。

Step $\textcolor{blue}{1}$：数量の関係を見つける。

Step $\textcolor{blue}{2}$：適当なものを文字で表して方程式をつくる。

Step $\textcolor{blue}{3}$：方程式を解く。

Step $\textcolor{blue}{4}$：解が問題にあっているか確認する。

※ $2$ 次方程式では、問題にあっていない解がよく出てくるので注意が必要です。

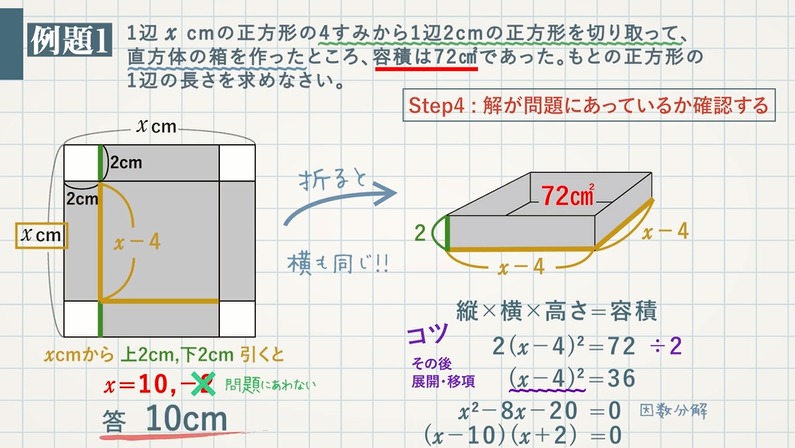
【例題 $\textcolor{green}{1}$ 】$\textcolor{green}{1}$ 辺 $\textcolor{green}{x{\rm cm}}$ の正方形の $\textcolor{green}{4}$ すみから $\textcolor{green}{1}$ 辺 $\textcolor{green}{2{\rm cm}}$ の正方形を切り取って、直方体の箱を作ったところ、容積は $\textcolor{green}{72{\rm cm}^2}$ であった。もとの正方形の $\textcolor{green}{1}$ 辺の長さを求めなさい。

Step $\textcolor{blue}{1}$：数量の関係を見つける。　

縦 $×$ 横 $×$ 高さ $=$ 容積

Step $\textcolor{blue}{2}$：適当なものを文字で表して方程式をつくる

$(x-4)×(x-4)×2=72$

Step $\textcolor{blue}{3}$：方程式を解く。

$2(x-4)^2=72$　これを解くと、$\textcolor{blue}{x=10,-2}$

Step $\textcolor{blue}{4}$：解が問題にあっているか確認する。

正方形１辺の長さが $x{\rm cm}$ ($x＞0$) なので、$\textcolor{blue}{x=-2}$ は問題にあわない。

よって、正方形 $1$ 辺の長さは $\textcolor{red}{10{\rm cm}}$

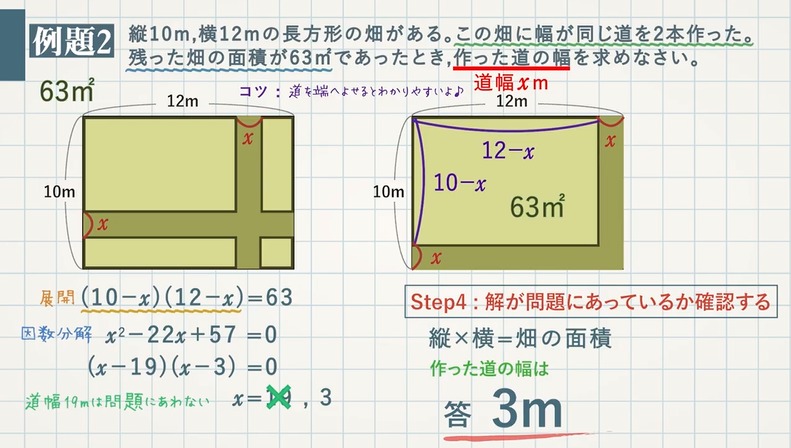
【例題 $\textcolor{green}{2}$ 】縦 $\textcolor{green}{10{\rm m}}$、横 $\textcolor{green}{12{\rm m}}$ の長方形の畑がある。この畑に幅が同じ道を $\textcolor{green}{2}$ 本作った。残った畑の面積が $\textcolor{green}{63{\rm m}^2}$ であったとき、作った道の幅を求めなさい。

Step $\textcolor{blue}{1}$：数量の関係を見つける。　

道の幅を $x{\rm m}$ とすると、縦 $×$ 横 $=$ 畑の面積

Step $\textcolor{blue}{2}$：適当なものを文字で表して方程式をつくる

　$(10-x)×(12-x)=63$

Step $\textcolor{blue}{3}$：方程式を解く。

　$(10-x)(12-x)=63$　これを解くと、$\textcolor{blue}{x=19,3}$

Step $\textcolor{blue}{4}$：解が問題にあっているか確認する。

道の幅が $x$ m ($x＜10$)なので、$\textcolor{blue}{x=19}$ は問題にあわない。よって、作った道の幅は $\textcolor{red}{3\rm m}$ となる。 

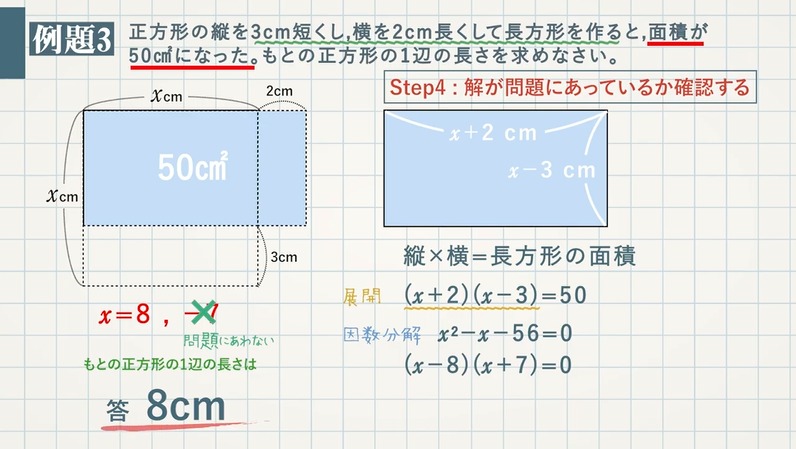
【例題 $\textcolor{green}{3}$ 】正方形の縦を $\textcolor{green}{3\rm cm}$ 短くし、横を $\textcolor{green}{2\rm cm}$ 長くして長方形を作ると、面積が $\textcolor{green}{50 \rm cm^2}$ になった。もとの正方形の $\textcolor{green}{1}$ 辺の長さを求めなさい。

Step $\textcolor{blue}{1}$：数量の関係を見つける。　

縦 $×$ 横 $=$ 長方形の面積

Step $\textcolor{blue}{2}$：適当なものを文字で表して方程式をつくる

　$(x+2)×(x-3)=50$

Step $\textcolor{blue}{3}$：方程式を解く。

　$(x+2)(x-3)=50$　これを解くと、$\textcolor{blue}{x=8,-7}$

Step $\textcolor{blue}{4}$：解が問題にあっているか確認する。

正方形の $1$ 辺の長さが $x \rm cm$  ($x＞0$) なので、$\textcolor{blue}{x=-7}$ は問題にあわない。よって、もとの正方形の $1$ 辺の長さは $\textcolor{red}{8\rm m}$ となる。