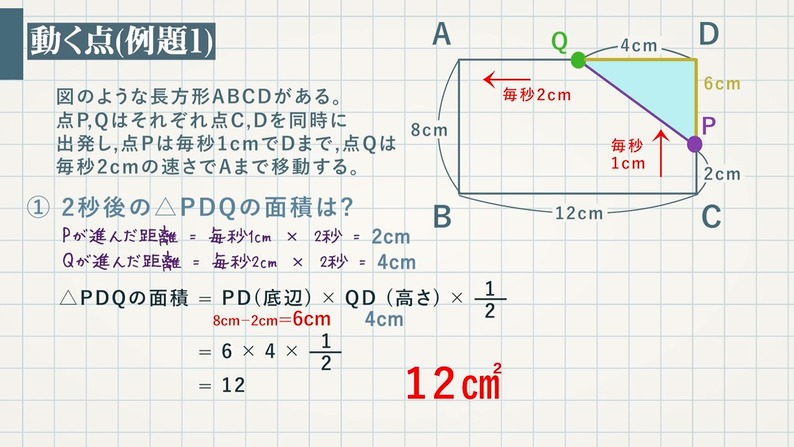
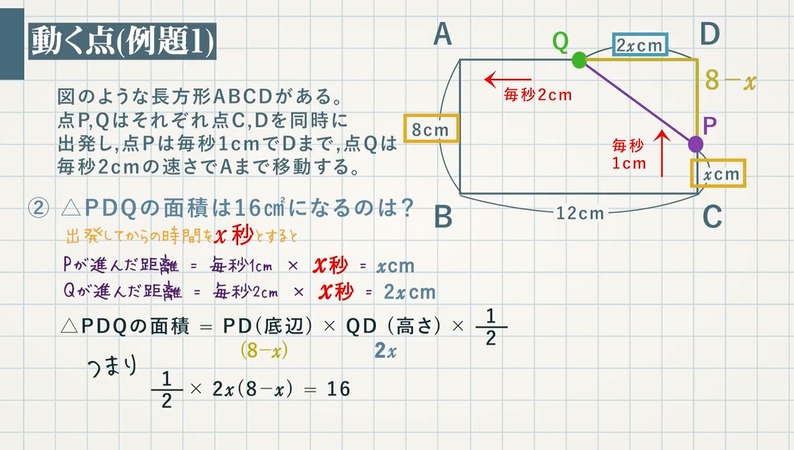
【例題 $\textcolor{green}{1}$ 】図のような長方形ABCDがある。点P、Qはそれぞれ点C、Dを同時に出発し、点Pは毎秒 $\textcolor{green}{1\rm cm}$ でDまで、点Qは毎秒 $\textcolor{green}{2\rm cm}$ の速さでAまで移動する。

① $\textcolor{green}{2}$ 秒後の△PDQの面積は？

Pが進んだ距離 $=$ 毎秒 $1\rm cm$  $×$ $2$ 秒 $=$ $2\rm cm$ 

Qが進んだ距離 $=$ 毎秒 $2\rm cm$ $×$ $2$ 秒 $=$ $4\rm cm$ 

\begin{eqnarray} △{\rm PDQ}の面積&=&{\rm PD} (底辺) × {\rm QD} (高さ) ×\frac{1}{2}\\ &=&6×4×\frac{1}{2}\\ &=&12　　　　　　　\textcolor{red}{12\rm cm^2} \end{eqnarray}

② △PDQに面積が $\textcolor{green}{16\rm cm^2}$ になるのは何秒後？

出発してからの時間を $\textcolor{blue}{x}$ 秒とすると、

Pが進んだ距離 $=$ 毎秒 $1\rm cm$  $×$ $x$ 秒 $=$ $x \rm cm$ 

Qが進んだ距離 $=$ 毎秒 $2\rm cm$  $×$ $x$ 秒 $=$ $2x\rm cm$ 

\begin{eqnarray} △{\rm PDQ}の面積&=&{\rm PD} (底辺) × {\rm QD} (高さ) ×\frac{1}{2}\\\frac{1}{2}×2x(8-x)&=&16　これを整理すると、\\x^2-8x+16&=&0　これを解くと、\textcolor{blue}{x=4}\newline\\　　　 \textcolor{red}{答え　 4 秒後}　\end{eqnarray}

【例題 $\textcolor{green}{2}$ 】図のような直角三角形ABCがある。点P、Qはそれぞれ点A、Bを同時に出発し、点PはBまで、点QはCまで動く。点P、Qが動いた長さを $\textcolor{green}{x 
\rm cm}$ とする。

△PBQの面積が $\textcolor{green}{9 \rm cm^2}$ になるのは？

\begin{eqnarray} △{\rm PBQ} の面積&=&{\rm PB} (底辺) × {\rm BQ} (高さ) ×\frac{1}{2}\\ &=&(9-x)×x×\frac{1}{2}\newline\\ \frac{1}{2}×x(9-x)&=&9　これを整理すると、\\ x^2-9x+18&=&0　これを解くと、\textcolor{blue}{x=3,x=6}\\\\　　 　\textcolor{red}{答え　3\rm cm , 6\rm cm} \end{eqnarray}