【例題①】図は、関数 $\textcolor{green}{y=ax^2}$ のグラフである。グラフ上を通る $\textcolor{green}{2}$ 点A,Bがあり、点Bの座標は（$\textcolor{green}{2,4}$）、点Aの $\textcolor{green}{y}$ 座標は $\textcolor{green}{25}$ である。このとき、次の問いに答えなさい。

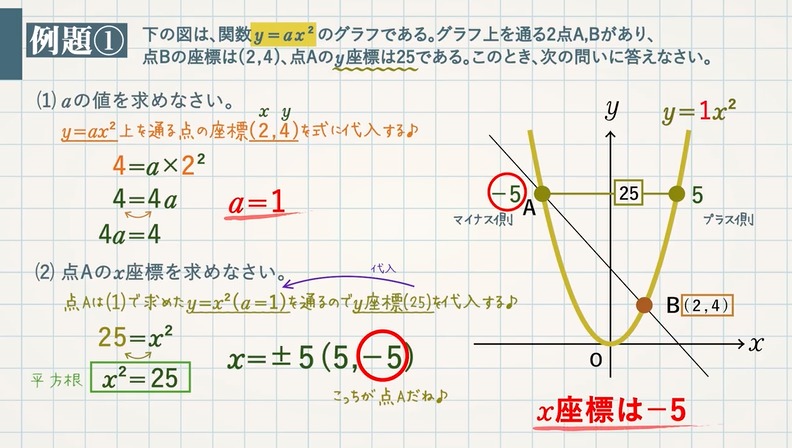
(1) $\textcolor{green}{a}$ の値を求めなさい。

$y=ax^2$ 上を通る点の座標（$2,4$）を式に代入します。

$4=a×2^2$　これを解いて、$\textcolor{Red}{a=1}$

(2) 点Aの $\textcolor{green}{x}$ 座標を求めなさい。

点Aは(1)で求めた $y=x^2 (a=1)$ を通るので、 $y$ 座標 $25$ を代入します。

$25=x^2$　これを解いて、$\textcolor{blue}{x=±5（5,-5）}$

図より、点Aの $x$ 座標はマイナス側となるので、点Aの $x$ 座標は $\textcolor{Red}{-5}$ となります。

【例題②】図のように、関数 $\textcolor{green}{y=\frac{1}{2}x^2…①}$ と関数 $\textcolor{green}{y=-x+4…②}$ のグラフがある。$\textcolor{green}{2}$ つのグラフが点A,Bで交わるとき、次の問いに答えなさい。

(1) 点A,Bの座標を求めなさい。

交点の求め方は $1$ 次関数の場合と同じ連立方程式の代入法で解きます。

\begin{eqnarray}  \begin{cases} y = \frac{1}{2}x^2 & \\ y = -x+4 & \end{cases} \end{eqnarray}

②を①に代入すると、

$-x+4=\frac{1}{2}x^2$　これを解いて、$\textcolor{blue}{x=-4,2}$

②の式に $x=-4,2$ を代入し、$y$ の値を求めます。

$y=-(-4)+4=\textcolor{blue}{8}$

$y=-2+4=\textcolor{blue}{2}$

よって、それぞれの座標は

A（$\textcolor{red}{-4,8}$）　　B（$\textcolor{red}{2,2}$）

(2) △AOBの面積を求めなさい。

今回は $\textcolor{blue}{y}$ 軸で三角形を $\textcolor{blue}{2}$ つにわける方法で解きます。

△AOB  $=$【黄色の三角形の面積】$+$【緑色の三角形】

【黄色の三角形の面積】

　 高さは $x$ 座標（絶対値）：$2$

　 底辺はOから②のグラフの切片：$4$

　 面積は、$4×4×\frac{1}{2}=\textcolor{blue}{8}$

【緑色の三角形】

　 高さは $x$ 座標（絶対値）：$2$

　 底辺は黄色の三角形と同じ：$4$

　 面積は、$2×4×\frac{1}{2}=\textcolor{blue}{4}$

よって、△AOBの面積 $=$ $8+4=\textcolor{red}{12}$