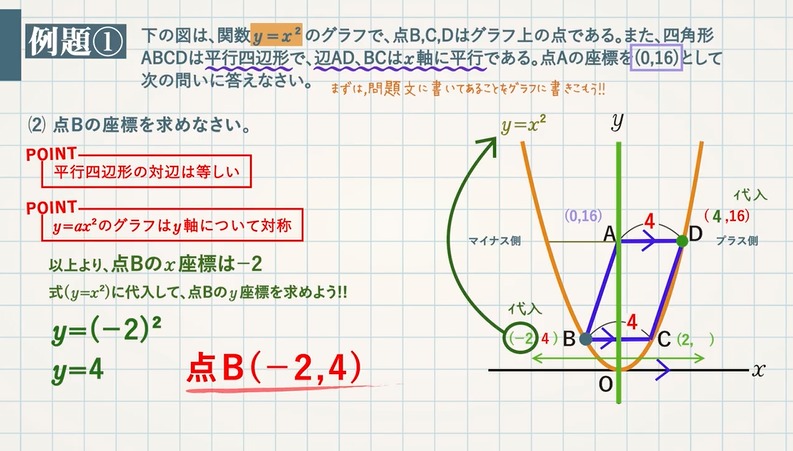
図は関数 $\textcolor{green}{y=x^2}$ のグラフで、点B,C,Dはグラフ上の点である。また、四角形ABCDは平行四辺形で、辺AD,BCは $\textcolor{green}{x}$ 軸について平行である。点Aの座標を（$\textcolor{green}{0,16}$）として、次の問いに答えなさい。

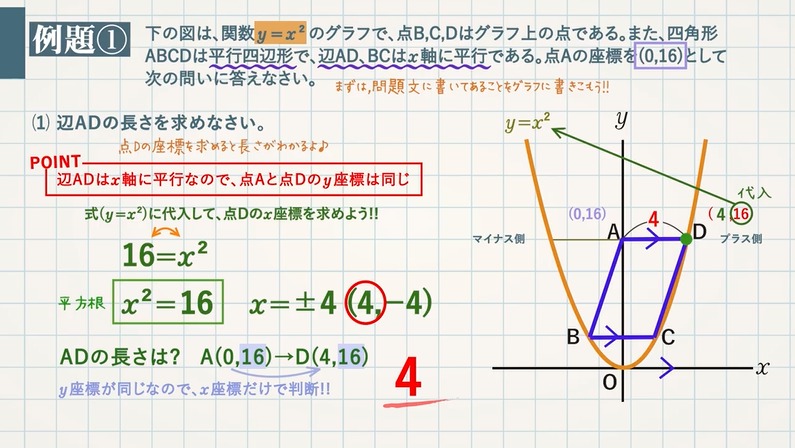
(1) 辺ADの長さを求めなさい。

まず、問題文に書いてあることをグラフに書き込みます。

点Aの座標が（$0,16$）とわかっているので、点Dの座標がわかれば、ADの長さを求めることができます。

POINT：辺ADは $\textcolor{blue}{x}$ 軸に平行なので、点A,点Dの $\textcolor{blue}{y}$ 座標は同じ

点Dは $y=x^2$ 上の点なので、$y=16$ を代入して $x$ 座標を求めます。

　$16=x^2$　これを解いて、$\textcolor{blue}{x=±4（+4,-4）}$

点Dの $x$ の値はプラス側なので、その $x$ 座標は $4$ 

よって、ADの長さは　$0→4$ より、$\bf {\textcolor{red}{4}}$ となります。

(2) 点Bの座標を求めなさい。

POINT：平行四辺形の対辺は等しい

POINT：$\textcolor{blue}{y=ax^2}$ のグラフは $\textcolor{blue}{y}$ 軸について対称

平行四辺形の対辺は等しいので、(1) AD $=\textcolor{blue}{4}$ より、BC $=\textcolor{blue}{4}$ となります。

また、$y=ax^2$ のグラフは $y$ 軸について対称なので、点B,Cの $x$ 座標はそれぞれ点B（$\textcolor{blue}{-2},　$） ,   点C（$2 ,　$）となります。

点Bは $y=x^2$ 上の点なので、$x=-2$ を代入して $y$ 座標を求めます。

　$y=(-2)^2$　これを解いて、${\textcolor{blue}{y=4}}$

よって、点B（$\textcolor{red}{-2,4}$）

図において、①は関数 $\textcolor{green}{y=x^2}$ 、②は関数 $\textcolor{green}{y=2x^2}$ のグラフである。①,②のグラフ上に四角形ABCDが正方形になるように $\textcolor{green}{4}$ 点A, B, C, D をとるとき, 次の問いに答えなさい。

(1) 点Aの座標を求めなさい。

点A（点D）の $x$ 座標を $t$ とすると、$y$ 座標はそれぞれの式に代入し、求めることができます。

点Aは $y=2x^2$ 上の点なので、$y=\textcolor{blue}{2t^2}$　点A（$t,2t^2$）

点Dは $y=x^2$ 上の点なので、$y=\textcolor{blue}{t^2}$　　点D（$t,t^2$）

POINT：$\textcolor{blue}{y=ax^2}$ のグラフは $\textcolor{blue}{y}$ 軸について対称

よって、点B,Cの座標は、点B（$-t,2t^2$）, 点C（$-t,t^2$）

POINT：正方形は、縦と横の長さが等しい

縦(AD) $=$ 横(AB) より、$t^2＝2t$ 　これを解いて、$t=0,2$

$0$ は適切でないので、$\textcolor{blue}{t=2}$

点A（$t,2t^2$）に $\textcolor{blue}{t=2}$ を代入　点A（$\textcolor{red}{2,8}$）