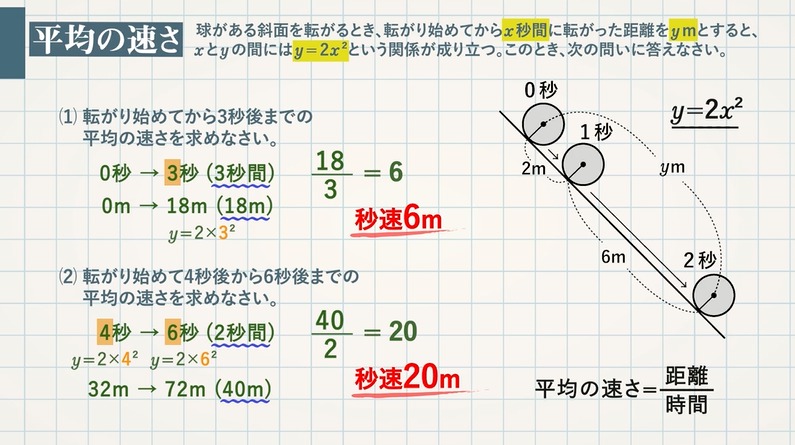
【問題】球がある斜面を転がるとき、転がり始めてから $\textcolor{green}{x}$ 秒間に転がった距離を $\textcolor{green}{y\rm m}$ とすると、$\textcolor{green}{x}$ と $\textcolor{green}{y}$ の間には $\textcolor{green}{y=2x^2}$ という関係が成り立つ。このとき、次の問いに答えなさい。 

(1) 転がり始めてから $\textcolor{green}{3}$ 秒後までの平均の速さを求めなさい。

\begin{eqnarray} 平均の速さ=\frac{距離}{時間} より\end{eqnarray}

時間：$0$ 秒 → $3$ 秒 ($\textcolor{blue}{3}$秒間)

距離：$0\rm m$ → $18\rm m$ ($\textcolor{blue}{18\rm m}$)　 $y=2x^2=2×3^2=18$

$\textcolor{blue}{\frac{18}{3}=6}$　秒速 $\textcolor{red}{6\rm m}$

(2) 転がり始めて $\textcolor{green}{4}$ 秒後から$\textcolor{green}{6}$ 秒後までの平均の速さを求めなさい。

時間：$4$ 秒 → $6$ 秒 ($\textcolor{blue}{2}$秒間)

距離：$32\rm m$ → $72\rm m$ ($\textcolor{blue}{40\rm m}$)

$y=2×4^2=32$ , $y=2×6^2=72$

$\textcolor{blue}{\frac{2}{40}=20}$　秒速 $\textcolor{red}{20\rm m}$

\begin{eqnarray} &\textcolor{blue}{平均}&\textcolor{blue}{の速さ=\frac{y の増加量}{x の増加量}=変化の割合} なので、\\&\textcolor{blue}{公式}&\textcolor{blue}{a×(q+p)}で求めることもできます\end{eqnarray}

【問題】時速 $\textcolor{green}{x\rm km}$ で走っている自動車がブレーキをかけたとき、ブレーキがきき始めてから止まるまでに進む距離(制動距離)を $\textcolor{green}{y\rm m}$ とすると、$\textcolor{green}{y}$ は $\textcolor{green}{x}$ の $\textcolor{green}{2}$ 乗に比例する。車が時速 $\textcolor{green}{50\rm km}$ で走っているときの制動距離が $\textcolor{green}{20\rm km}$ とする。

(1) $\textcolor{green}{y}$ を $\textcolor{green}{x}$ の式で表しなさい。

$y$ は $x$ の $2$ 乗に比例し、車が時速 $50{\rm km } (x)$ で走っているときの 制動距離が $20{\rm m} (y)$ なので、$y=ax^2$ に $\textcolor{blue}{x=50}$ , $\textcolor{blue}{y=20}$ を代入 

$\textcolor{blue}{20}=a×\textcolor{blue}{50}^2$　これを解いて、$\textcolor{blue}{a=\frac{1}{125}}$　

よって、$\textcolor{red}{y=\frac{1}{125}x^2}$

(2) 時速が $\textcolor{green}{75\rm km}$ のときの制動距離は何 $\textcolor{green}{\rm m}$ になりますか。

$\textcolor{blue}{x=75}$ を (1) で求めた $y=\frac{1}{125}x^2$ に代入

$y=\frac{1}{125}×\textcolor{blue}{75}^2$　これを解いて、$\textcolor{blue}{y=45}$

よって、$\textcolor{red}{45\rm m}$

【問題】電車がA地点を出発してから $x$ 秒間に進む距離を $\textcolor{green}{y\rm m}$ とすると、$\textcolor{green}{y=\frac{1}{2}x^2}$ の関係がある。また、電車が出発すると同時に、A地点を秒速 $\textcolor{green}{15\rm m}$ で通過する自動車がある。このとき、次の問いに答えなさい。

(1) 自動車がA地点を通過してから $\textcolor{green}{x}$ 秒間に進む距離を $\textcolor{green}{y\rm m}$ として、グラフをかきなさい。

原点(A地点)を通る比例のグラフになります。

秒速 $15\rm m$ なので、例えば $\textcolor{blue}{40}$ 秒ならば、$15×40=\textcolor{blue}{600\rm m}$ 進む。よって、座標($\textcolor{blue}{40,600}$) と原点を通る直線をひく。直線の式は  $\textcolor{red}{y=15x}$

(2) 自動車が電車に追いつかれるのは、何秒後か？

追いつく$=$ 交点を連立方程式の代入法で求める。

\begin{eqnarray} \begin{cases} y = \frac{1}{2}x^2 & \\ y=15x & \end{cases}　\frac{1}{2}x^2=15x　\end{eqnarray}

変形すると、$x^2-30x=0$　これを解いて $\textcolor{blue}{x=0,30}$

$0$ は問題に適していないので、$\textcolor{blue}{x=30}$

よって、自動車が電車に追いつかれるのは、出発から $\textcolor{red}{30}$ 秒後である。