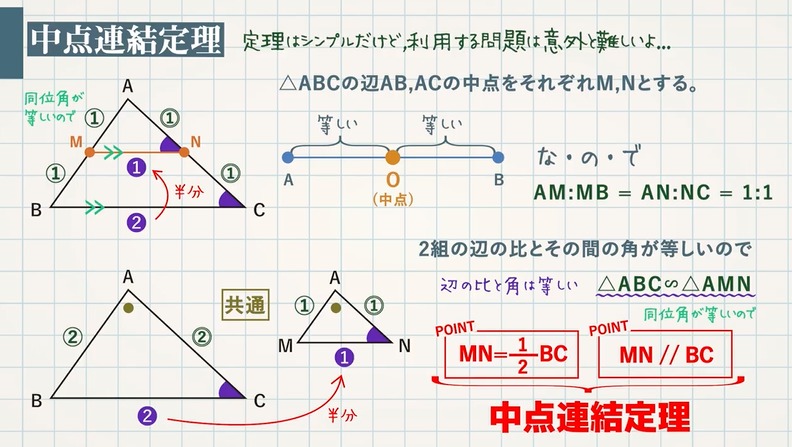
$\rm △ABC$ の辺 $\rm AB,AC$ の中点をそれぞれ $\rm M,N$ とする。中点は、両端から等しい位置にある点なので、$\textcolor{blue}{\rm AM:MB=AN:NC=1:1}$

$\rm △ABC$ と $\rm △AMN$ において、

$\textcolor{blue}{\rm AB:AM=2:1}$…①

$\textcolor{blue}{\rm AC:AN=2:1}$…②

$\textcolor{blue}{\rm ∠A}$ は共通…③

①,②,③ より、$2$ 組の辺の比とその間の角が等しいので、$\textcolor{blue}{\rm △ABC∽△AMN}$ 

相似な図形の対応する辺の長さの比は等しいので、$\textcolor{blue}{\rm BC:MN=2:1}$ より、$\textcolor{blue}{\rm MN=\frac{1}{2}BC}$

また、相似な図形の対応する角の大きさは等しいので、$\textcolor{blue}{\rm ∠ACB=∠ANM}$。同位角が等しいので、$\textcolor{blue}{\rm MN//BC}$

このような中点を結んだ線分について成り立つ性質を中点連結定理といいます。$\textcolor{blue}{\rm POINT:MN=\frac{1}{2}BC}$  ,  $\textcolor{blue}{\rm MN//BC}$

【 Level $\textcolor{green}{1}$ 】図の $\textcolor{green}{\rm M,N}$ がそれぞれの辺の中点であるとき、$\textcolor{green}{x,y}$ の値を求めなさい。

(1) $\textcolor{blue}{\rm BC=2MN} $より、$x=6×2=\textcolor{red}{12}$

　  $\textcolor{blue}{\rm MN//BC}$ より、同位角は等しいので、$y=\textcolor{red}{60}$

(2) $\textcolor{blue}{\rm MN=\frac{1}{2}AB} $より、$x=18×\frac{1}{2}=\textcolor{red}{9}$

　  $\textcolor{blue}{\rm MN//BC}$ より、$\rm ∠MNC=∠ABC$

　  三角形の内角の和は$180°$。$y=180-74-34=\textcolor{red}{72}$

【 Level $\textcolor{green}{2}$ 】 次の長さを求めなさい。

(1) $\textcolor{green}{\rm△DEF}$ の周の長さ($\textcolor{green}{\rm D,E,F}$ はそれぞれの辺の中点) 

$\rm DE=\frac{1}{2}AC$ より、$10×\frac{1}{2}=\textcolor{blue}{5\rm  cm}$

$\rm EF=\frac{1}{2}AB$ より、$16×\frac{1}{2}=\textcolor{blue}{8\rm  cm}$

$\rm DF=\frac{1}{2}BC$ より、$14×\frac{1}{2}=\textcolor{blue}{7\rm  cm}$

よって、$\rm DE+EF+DF=\textcolor{red}{20 cm}$

(2) 線分$\textcolor{green}{\rm GC}$の長さ($\textcolor{green}{\rm D,E}$は $\textcolor{green}{\rm AB}$を $\textcolor{green}{3}$ 等分、$\textcolor{green}{\rm F}$は $\textcolor{green}{\rm BC}$の中点)

$\rm DC=2EF$ より、$12×2=\textcolor{blue}{24\rm  cm}$

$\rm DG=\frac{1}{2}EF$ より、$12×\frac{1}{2}=\textcolor{blue}{6\rm  cm}$

よって、$\rm DC-DG=\textcolor{red}{18 cm}$

【 Level $\textcolor{green}{3}$ 】図の四角形$\textcolor{green}{\rm ABCD}$ は $\textcolor{green}{\rm AB=CD}$ である。辺 $\textcolor{green}{\rm AD,BC}$ の中点をそれぞれ $\textcolor{green}{\rm E,F}$ 対角線 $\textcolor{green}{\rm B,D}$ の中点を $\textcolor{green}{\rm G}$ とするとき、$\textcolor{green}{\rm △EGF}$ が二等辺三角形であることを証明しなさい。 

$\rm △ABD$ において、$\rm E,G$ は $\rm AD,BC$ の中点なので、中点連結定理より、$\textcolor{blue}{\rm EG=\frac{1}{2}AB}$…①

$\rm △BCD$ においても同様に、$\textcolor{blue}{\rm FG=\frac{1}{2}CD}$…②

また、仮定より、$\textcolor{blue}{\rm AB=CD}$…③

①,②,③ より$\rm △EGF$ は対辺が等しい($\textcolor{blue}{\rm EG=FG}$) ので、二等辺三角形である。

【 Level $\textcolor{green}{3}$ 】図の四角形 $\textcolor{green}{\rm ABCD}$ の辺 $\textcolor{green}{\rm AB,BC,CD,DA}$ の中点をそれぞれ $\textcolor{green}{\rm E,F,G,H}$ とするとき、四角形 $\textcolor{green}{\rm EFGH}$ が平行四辺形であることを証明しなさい。

いろいろな解き方があるけど、今回は対角線をひく方法で解きます。

対角線 $\rm AC$ をひく。

$\rm △ABC$ において、$\rm E,F$  は $\rm AB,BC$ の中点なので、中点連結定理より、$\textcolor{blue}{\rm EF//AC,EF=\frac{1}{2}AC}$ …①

$\rm △ADC$ においても同様に、$\textcolor{blue}{\rm GH//AC,GH=\frac{1}{2}AC}$ …②

①,②より、$\textcolor{blue}{\rm EF//GH,EF=GH}$

よって、$1$ 組の向かい合う辺が等しく平行なので、四角形 $\rm EFGH$ は平行四辺形である。