わり算のことを除法といい、その結果を商といいます。除法では、わる数を逆数にして、乗法になおして計算することができます。

$\textcolor{blue}{2}$ 数の積が $\textcolor{blue}{1}$ になる時、一方の数を他方の数の逆数という。

　例：$\frac{2}{3}→\frac{3}{2}　　-\frac{2}{3}→-\frac{3}{2}$

$-6÷2$ は $－6× \frac{1}{2}$という乗法になおすことができます。

$－6÷2＝－6× \frac{1}{2}＝－3$

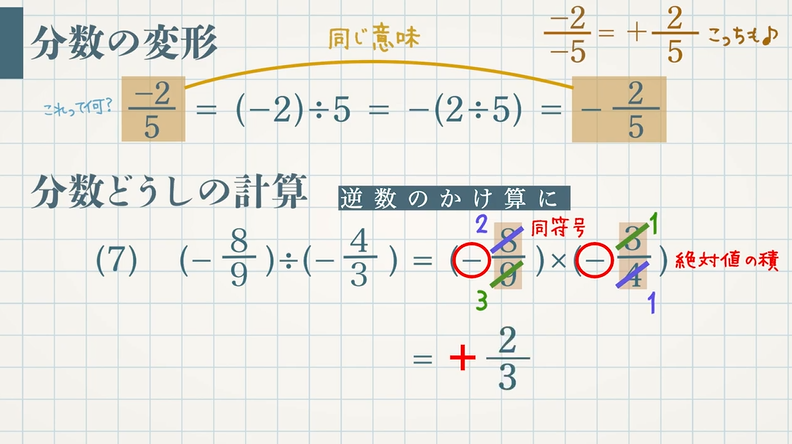
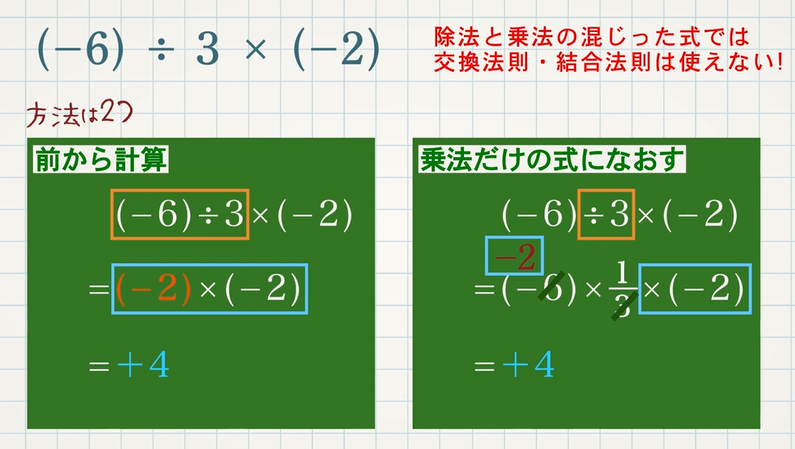
乗法に変形できるということは、除法の符号のルールは乗法と同じになります。よって、正の数、負の数の除法については次のことがいえます。

同符号（＋どうし,－どうし）の $\textcolor{blue}{2}$ 数の商

符号：正の符号（$\textcolor{blue}{+}$）　絶対値：$\textcolor{blue}{2}$ 数の絶対値の商

異符号（$\textcolor{blue}{＋}$と$\textcolor{blue}{－}$ , $\textcolor{blue}{－}$と$\textcolor{blue}{＋}$）の $\textcolor{blue}{2}$ 数の商

符号：負の符号（－）　絶対値： $\textcolor{blue}{2}$ 数の絶対値の商

【問題】次の計算をしなさい。

(1) $\textcolor{green}{(+56)÷(+8)}=+(56÷8)=\textcolor{red}{+7}$　同符号

(2) $\textcolor{green}{(-18)÷(+2)}=-(18÷2)=\textcolor{red}{-9}$　異符号

(3) $\textcolor{green}{(-90)÷(-15)}=+(90÷15)=\textcolor{red}{+6}$　同符号

(4) $\textcolor{green}{(+2)÷(-6)}=-(2÷6)=\textcolor{red}{-\frac{1}{3}}$　異符号

分数をふくむ除法について確認しましょう。

まずは分数の表し方です。下の $2$ つは同じ数を表しますが、ふつうは$-\frac{2}{5}$ と書きます。

$　\frac{-2}{5}=(-2)÷5=-(2÷5)=\textcolor{blue}{-\frac{2}{5}}$

分数をふくむ除法では、除法を乗法になおして計算します。（逆数のかけ算に）

$　　 (-\frac{8}{9})÷(-\frac{4}{3})$　　乗法になおす

$　=(-\frac{8}{9})×(-\frac{3}{4})$　　同符号, 絶対値の積

$　=\textcolor{red}{+\frac{2}{3}}$

乗法と除法の混じった式の計算のしかたについて考えましょう。

【例題】$\textcolor{green}{(-6)÷3×(-2)}$ を計算しなさい。

乗法と除法の混じった式では交換法則・結合法則は使えません。（乗法だけの式になおせば使えます）

計算方法が $2$ つあるので、それぞれ確認しておきましょう。

① 前から計算

$　\textcolor{green}{(-6)÷3×(-2)}=(-2)×(-2)=\textcolor{red}{+4}$

② 乗法だけの式になおす

$　\textcolor{green}{(-6)÷3×(-2)}=(-6)×\frac{1}{3}×(-2)=\textcolor{red}{+4}$