食パンの $1$ つの値段を $x$ 円、タピオカミルクティーの$1$ つの値段を $y$ 円とすると、
食パン $2$ つとタピオカミルクティー $3$ つの代金が $2100$ 円は、
$\textcolor{blue}{2x+3y=2100}$
食パン $2$ つとタピオカミルクティー $1$ つの代金が $1100$ 円は、
$\textcolor{blue}{2x+y=1100}$
とそれぞれ式に表すことができます。
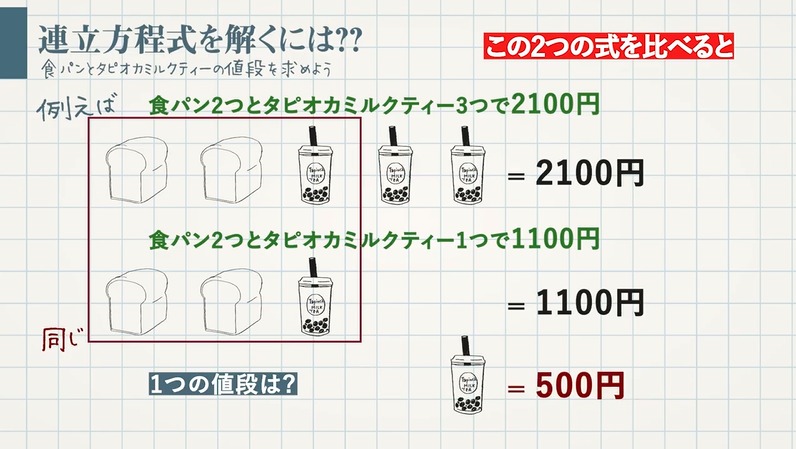
食パンの $1$ つの値段を $x$ 円、タピオカミルクティーの$1$ つの値段を $y$ 円とすると、
食パン $2$ つとタピオカミルクティー $3$ つの代金が $2100$ 円は、
$\textcolor{blue}{2x+3y=2100}$
食パン $2$ つとタピオカミルクティー $1$ つの代金が $1100$ 円は、
$\textcolor{blue}{2x+y=1100}$
とそれぞれ式に表すことができます。

さきほどの $2$ つの方程式を連立方程式の形に表すと、
\begin{eqnarray} \left\{ \begin{array}{l} 2x+3y=2100 ・・・①\\ 2x+y =1100 ・・・② \end{array} \right. \end{eqnarray}
①の式から②の式を引く
\begin{eqnarray} 2x+3y&=&2100\\ -) 2x+y&=&1100\\ \hline 2y&=&1000\\ \textcolor{blue}{y}&\textcolor{blue}{=}&\textcolor{blue}{500} \end{eqnarray}
$\textcolor{blue}{y=500}$ を②の式に代入して、$\textcolor{blue}{x=300}$
よって、$\textcolor{red}{(x,y)=(5,1)}$
連立方程式を解くのに、左辺どうし、右辺どうしをそれぞれたすかひくかして、 $1$ つの文字を消去して解く方法を加減法といいます。

下のように係数が等しくないときは、式を何倍かして係数の絶対値をそろえます。
\begin{eqnarray} \left\{ \begin{array}{l} x+3y=8 ・・・①\\ 2x-5y =5 ・・・② \end{array} \right. \end{eqnarray}
$x$ の係数の絶対値をそろえるために①の式を $\textcolor{blue}{2}$ 倍します
\begin{eqnarray} 2x+6y&=&16 \\ -) 2x-5y&=&5 \\ \hline 11y&=&11\\ \textcolor{blue}{y}&\textcolor{blue}{=}&\textcolor{blue}{1} \end{eqnarray}
$\textcolor{blue}{y=1}$ を①の式に代入して、$\textcolor{blue}{x=5}$
よって、$\textcolor{red}{(x,y)=(5,1)}$

【問題】 $\textcolor{green}{y}$ を消去するために、①の式を $\textcolor{green}{2}$ 倍しました。②の式は何倍すればいいでしょうか。
\begin{eqnarray} \left\{ \begin{array}{l} 4x+3y=2 ・・・①×2\\ 3x-2y =10 ・・・②×□ \end{array} \right. \end{eqnarray}
②の式を $\textcolor{red}{3}$ 倍すれば $y$ の係数の絶対値が $\textcolor{blue}{6}$ でそろいます。
\begin{eqnarray} 8x+6y&=&4\\ +) 9x-6y&=&30\\ \hline 17x&=&34\\ \textcolor{blue}{x}&\textcolor{blue}{=}&\textcolor{blue}{2}\\ \end{eqnarray}
$x=2$ を①の式に代入して、$\textcolor{blue}{y=2}$
よって、$\textcolor{red}{(x,y)=(2,-2)}$
コンテンツやシステムに関するお問い合わせ・オファーはこちらから