平方根の考えを使う解き方-２次方程式：中学３年生

平方根の考えを使う解き方

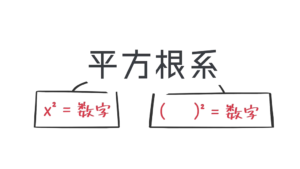「平方根の考え方を使う解き方」をみていきましょう。パターンは, 「$\rm x^2=$ 数字」と「$\rm (　　)^2=$ 数字」の２種類でなります。さらにこの２つは, 解き方・流れが同じなので, 違いさえ理解していたら実質１パターンの把握でOKですね。

「$\rm x^2=$ 数字」の解き方

大問５。まずは「$\rm x^2=$ 数字」から確認しましょう。

重要なのは, やはりこの形になります。因数分解系が「$\rm =0$」の形であったのに対し, 平方根系は「$\rm x^2=$」の形にしないといけません。

(1)はすでにその形になっています。(2)はなってないので, 整理しましょう。両辺を $\rm 5$ で割って $\rm x^2=9$。

この形ができれば, あとは左辺は２乗をはずして $\rm x^2 → x$。右辺は数字の“平方根”を答えるだけです。(１)だと $\rm 7$ の平方根なんで $±\sqrt{7}$ 。(２)だと $\rm 9$ の平方根なんで $\rm ±3$ 。

“平方根”なので, $\rm √$ があるかないかに関わらず「$\rm ±$」は常に必要なので忘れないようにしましょう。ここでも解は $\rm +$ 側と $\rm -$ 側で“２つ”あります。

(3),(4)は分数が含まれる問題です。

「$\rm x^2=$」の形を作りたいので, まずは $-9$ や $-21$ を移項する。そして, $\rm x^2$ の前に付いてる数字で全体を割ります。

割り切れないときは分数ですね。整理して「$\rm x^2=$」の形を作ります。

(4)については, “約分”できますが, このままの方が楽なので置いておきましょう。分母に $\rm √$ が残ると最終的に“有理化”しないといけないので, このまま平方根を求めた方が楽です。

分数の平方根は“分母・分子”それぞれを考えればいいだけですね。(３)は分母が $\rm 2$ で分子が $\rm 3$ 。(４)は分母の $\rm √$ が外れて $\rm 3$ , 分子は $\rm 21$ の平方根なので $\sqrt {21}$。

ここも同じやり方なんでサラっとだけ見ていきましょう。

まずは移項です。そして, $\rm x^2$ の前に数字があれば, その数で全体を割る。「$\rm x^2=$」の形ができたら, 左辺は $\rm x$ にして右側に“平方根”を書く。そういう流れですかね。

ただ, (6)は $\rm √$ の中を簡単にできるので, 変形が必要です。$\sqrt{12}$ は $\rm 2^2$ が外に出るので, $2\sqrt{3}$ になります。

「$\rm (　　)^2=$ 数字」の解き方

大問６。こちらは「$\rm (　　)^2=$」の形ですね。

これらの問題は, もともと「$\rm (　　)^2=$」の形になっているので, 移項などはありません。

やることはさっきと同じで, 左辺は「$\rm (　　)^2$」を外して, 右辺に“平方根”を書く。大問５との違いは, 左側に数字が残ってるということですね。この数字を右辺に移項してあげれば終わりです。数字は $±$ の前に入れましょう。

ただ, (2)みたいに平方根が $\rm √$ じゃない場合は計算しないといけません。解は２つなので, 「$\rm +$」と「$\rm -$」で分けて計算しましょう。$2+3=5$ と $2-3=-1$ ですね。

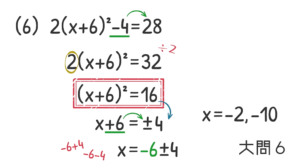最後に(6)をみておきましょう。

この問題は「$\rm (　　)^2=$」の形になっていないので, 初めに変形しましょう。順番はいつも通り, まずは移項です。次に, $x^2$ の係数 $2$ で両辺（全体）を割ってあげる。

「$\rm (　　)^2=$」の形ができれば, 左辺の「$\rm (　　)^2$」を外して, 右側には平方根を書く。左辺の $\rm 6$ を移項して, 今回も計算です。$-6+4=-2$ と $-6-4=-10$ になります。

「因数分解」と「平方根」の見分け方

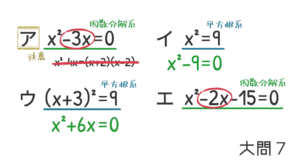最後に大問７。「$\rm -3$」を解にもつものを選びなさい。という問題ですね。

パッと見て, ア・イ・ウ・エの式がそれぞれ「因数分解系」か「平方根系」かわかりますか？

ア,エが因数分解。イ, ウが平方根系になります。「$\rm =0$」とか「２乗$\rm =$」っていう基本的な形なので, わかりやすいかなぁと思います。

見分けるコツとしては「～$\rm x$」のような１次の文字が入ってると因数分解系です。少し式を変形されて難しかったとしても, この点を意識して判断してもらえればと思います。「～$\rm x$」があるが因数分解で解けない問題は「解の公式」を使う流れになります。

イとウも整理すると「因数分解」で解けちゃうんですけど, 「～$\rm x$」が無かったら, 「平方根」のアプローチで解いてみてOKだと思います。

それぞれ解くと, 「$\rm -3$」を解にもつのはイとエになります。

以上が平方根の考えを使った解き方, 計算方法の見分け方になります。

解説動画はコチラ↓

各PDFはコチラ↓
問題
https://ecommons.biz/wp-content/uploads/2021/10/R17-01-1.pdf
解答欄
https://ecommons.biz/wp-content/uploads/2021/10/R17-01-2.pdf
解答
https://ecommons.biz/wp-content/uploads/2021/10/R17-01-3.pdf

関連記事はコチラ↓
因数分解を使った解き方
https://ic0.tv/press/r17-1-1/
平方完成を使った解き方
https://ic0.tv/press/r17-1-3/
解の公式を使った解き方
https://ic0.tv/press/r17-1-4/
２次方程式の計算まとめ
https://ic0.tv/press/r17-1-5/

デジタル板書データはコチラ↓
因数分解による解き方
https://ic0.tv/class/mathematics/middle-school/016/nijihoteishiki-insubunkai/
平方根の考えを使った解き方
https://ic0.tv/class/mathematics/middle-school/016/nijihoteishiki-heihokon/