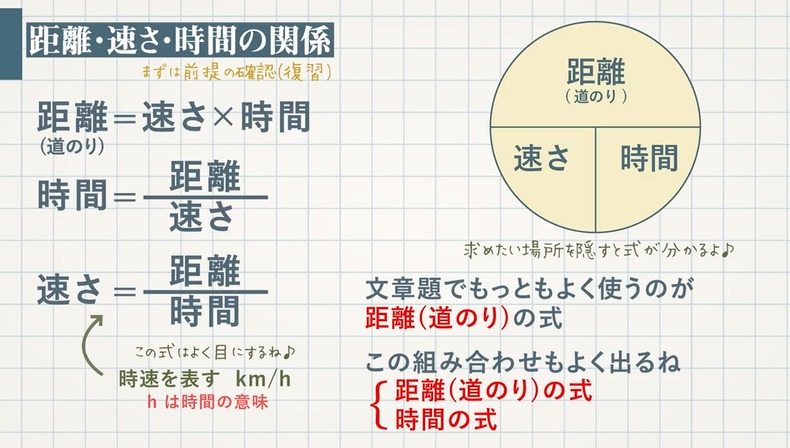
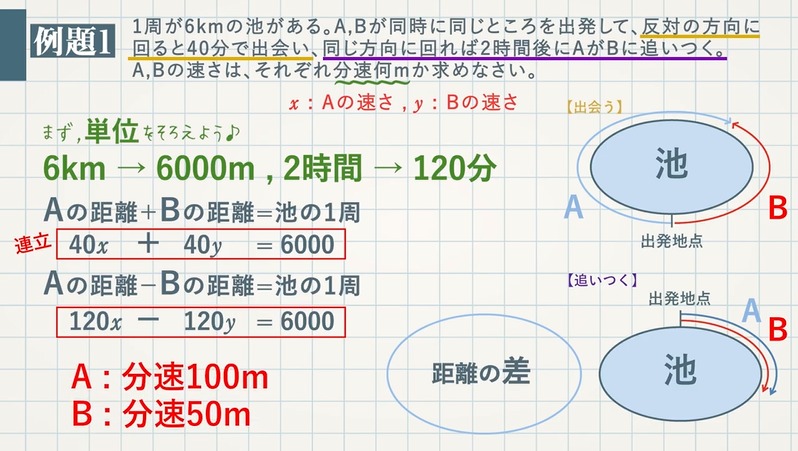
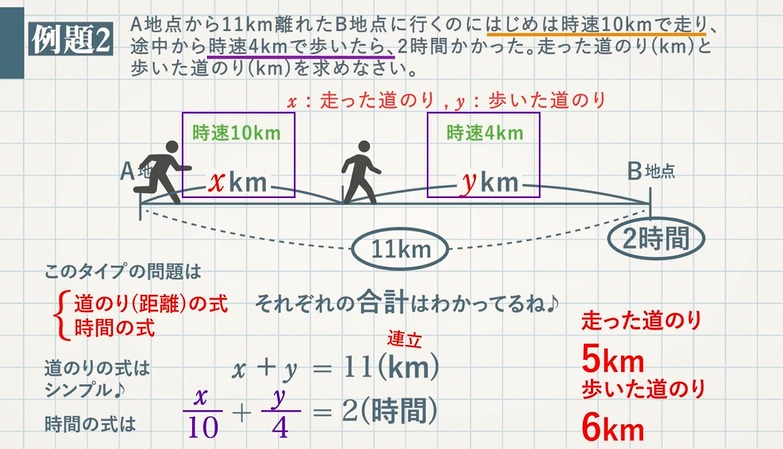
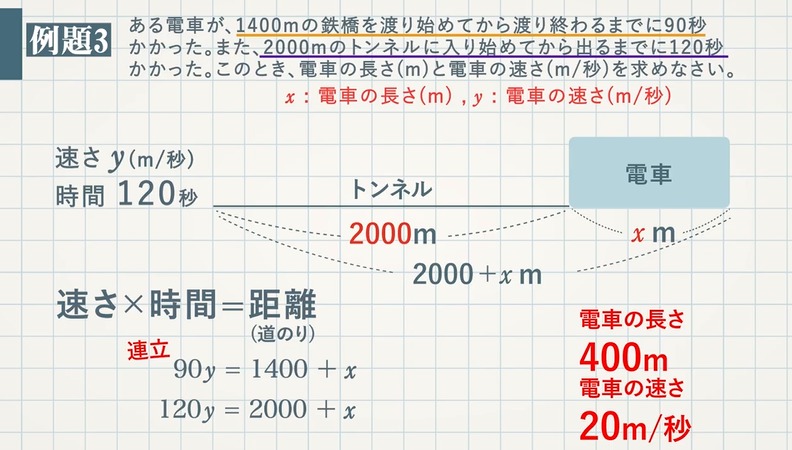
【例題 $\textcolor{green}{1}$ 】 $\textcolor{green}{1}$ 周が $\textcolor{green}{6\rm km}$ の池がある。A,Bが同時に同じところを出発して、反対の方向に回ると $\textcolor{green}{40}$ 分で出会い、同じ方向に回れば $\textcolor{green}{2}$ 時間後にAがBに追いつく。A,Bの速さはそれぞれ分速何 $\textcolor{green}{\rm m}$ か求めなさい。
Aの速さを分速 $x\rm m$ ,Bの速さを分速 $y\rm m$ とすると、
$40$ 分で出会う$=$ Aの進んだ距離 $+$ Bの進んだ距離
和が池 $\textcolor{blue}{1}$ 周 $\textcolor{blue}{40x+40y=6000}$
$2$ 時間($120$分)で追いつく$=$Aの進んだ距離$-$Bの進んだ距離
差が池 $\textcolor{blue}{1}$ 周 $\textcolor{blue}{120x-120y=6000}$
$2$ つの方程式を連立
\begin{eqnarray} \left\{ \begin{array}{l} 40x + 40y = 6000 \\ 120x – 120y = 6000 \end{array} これを解くと\textcolor{blue}{(x , y)=(100 , 50)} \right. \end {eqnarray}
よって、Aは分速 $\textcolor{Red}{100\rm m}$
Bは分速 $\textcolor{red}{50\rm m}$