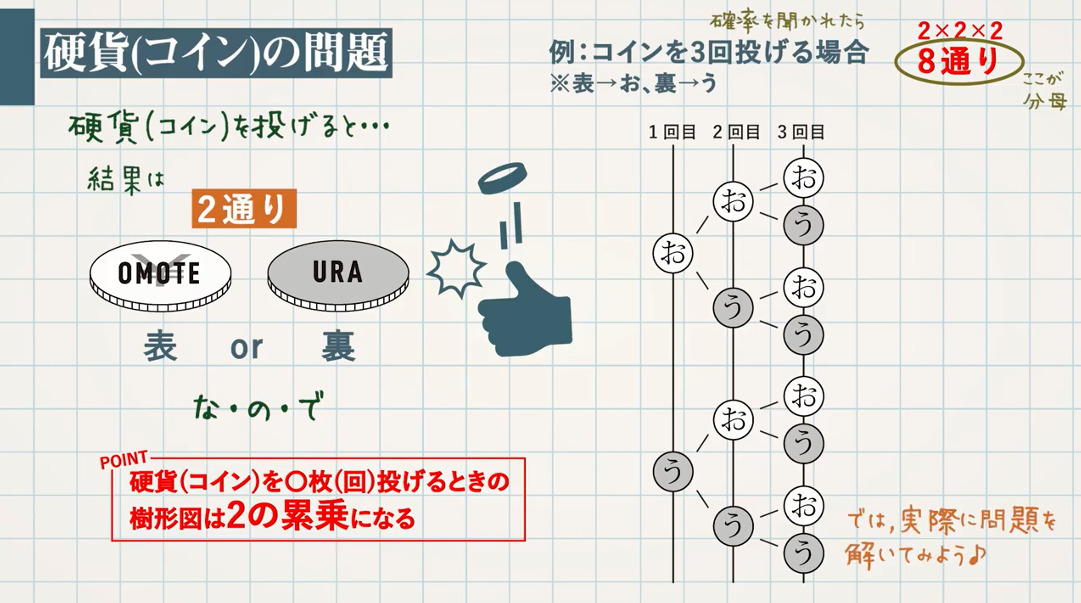
硬貨（コイン）を投げると、結果は表 or 裏なので、$2$ 通り。

POINT：硬貨（コイン）を〇枚（回）投げるときの樹形図は $\textcolor{blue}{2}$ の累乗になる。

例：コインを $3$ 回投げる場合

※表→お、裏→う として樹形図を作成

$1$ 回目は、$\textcolor{blue}{2^1=2}$ 通り

$2$ 回目は、$\textcolor{blue}{2^2=4}$ 通り

$3$ 回目は、$\textcolor{blue}{2^3=8}$ 通り　となります。

コインを $3$ 回投げるときの問題で確率を聞かれたら、分母は $\textcolor{blue}{8}$ になります。

では、実際の問題を解いてみましょう。

$\textcolor{green}{3}$ 枚の硬貨を同時に投げるとき、次の問いに答えなさい。

(1) 表裏の出方は全部で何通りあるか求めなさい。

さっきの樹形図で考えましょう。　$2^3=\textcolor{red}{8}$ 通り

(2) $\textcolor{green}{1}$ 枚が表、$\textcolor{green}{2}$ 枚が裏となる確率を求めなさい。

分母になるのは、(1) で求めた $\textcolor{blue}{8}$ 通り

$1$ 枚が表、$2$ 枚が裏となるのは、（表、裏、裏）（裏、表、裏）（裏、裏、表）の $\textcolor{blue}{3}$ 通り。よって、その確率は $\textcolor{red}{\frac{3}{8}}$

(3) 少なくとも $\textcolor{green}{1}$ 枚が裏となる確率を求めなさい。

少なくとも $1$ 枚が裏というのは、裏が $1$ 枚以上のときです。

$1$ 枚以上になるのは、（表、表、裏）（表、裏、表）（表、裏、裏）（裏、表、表）（裏、表、裏）（裏、裏、表）（裏、裏、裏）の $\textcolor{blue}{7}$ 通り。よって、その確率は $\textcolor{red}{\frac{7}{8}}$

(4) $\textcolor{green}{100}$ 円玉、$\textcolor{green}{50}$ 円玉、$\textcolor{green}{10}$ 円玉が $\textcolor{green}{1}$ 枚ずつある。この $\textcolor{green}{3}$ 枚の硬貨を同時に投げるとき、表が出た硬貨の合計金額が $\textcolor{green}{60}$ 円以上となる確率を求めなさい。

$3$ 枚の硬貨なので、樹形図は同じになります。

POINT：それぞれの回が何円玉かを決める

お（表）の部分の金額を計算すると $60$ 円以上になるのは、

（表、表、表）$=100+50+10=160$ 円

（表、表、裏）$=100+50=150$ 円

（表、裏、表）$=100+10=110$ 円

（表、裏、裏）$＝100$ 円

（裏、表、表）$=50+10=60$ 円　の $\textcolor{blue}{5}$ 通り。

よって、その確率は $\textcolor{red}{\frac{5}{8}}$

(5) 数直線上の原点に点 $\textcolor{green}{\rm P}$ がある。硬貨を $\textcolor{green}{1}$ 枚投げ、表が出れば点 $\textcolor{green}{\rm P}$ は正の方向に $\textcolor{green}{2}$ 移動し、裏が出れば負の方向に $\textcolor{green}{1}$ 移動する。硬貨を $\textcolor{green}{3}$ 回投げるとき、点 $\textcolor{green}{\rm P}$ が原点にある確率を求めなさい。

硬貨を $3$ 回なので、樹形図は同じになります。

組合せとしては、

表 $3$ 回、裏 $0$ 回　$2+2+2=6$

表 $2$ 回、裏 $1$ 回　$2+2-1=3$

表 $1$ 回、裏 $2$ 回　$2-1-1=\textcolor{blue}{0}$ ←原点

表 $0$ 回、裏 $3$ 回　$-1-1-1=-3$

表 $1$ 回、裏 $2$ 回になるのは、

（表、裏、裏）（裏、表、裏）（裏、裏、表）の $\textcolor{blue}{3}$ 通り。

よって、その確率は $\textcolor{red}{\frac{3}{8}}$