まずは絶対値について中学校の復習をしておきましょう。

絶対値

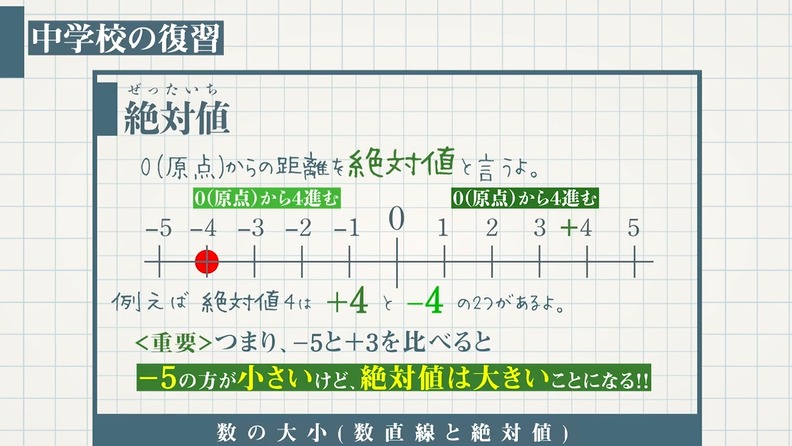
$0$（原点）からの距離を絶対値といいます。

例えば、絶対値 $4$ は $+4$ と $-4$ の $2$ つがあります。

＜重要＞

$-5$ と $+3$ を比べると、

$-5$ の方が数としては小さいけど、絶対値は大きいことになります。

高校では、実数 $a$ の絶対値を $|a|$  と表します。

$a≧0$ のとき、$|a|=a$

（$0$ や正の数のとき、そのまま）

$a≦0$ のとき、$|a|=-a$

（負の数のとき、符号が変わる）

例：$\textcolor{green}{|2|}=\textcolor{red}{2}$

　　$\textcolor{green}{|-2|}=\textcolor{red}{2}$　　※絶対値に（$\textcolor{blue}{-}$）はありません。

これは、$2$ と $-2$ の絶対値は $2$ になるっていうだけで、中学で習ったことと変わりません。

$|0.5|=0.5$ 　$0.5$ の絶対値は $0.5$

$|-100|=-(-100)=100$　$-100$ の絶対値は $100$

【例題】次の値を求めなさい。

(1) $\textcolor{green}{|-6+3|}$

$=|-3|$

$=\textcolor{red}{3}$

(2) $\textcolor{green}{|2|-|-5|}$

$=\textcolor{blue}{2}-\textcolor{blue}{5}$

$=\textcolor{Red}{-3}$

(3) $\textcolor{green}{|\sqrt{3}-2|}$

$=\textcolor{blue}{-}(\sqrt{3}-2)$　※$\sqrt{3}-2$ は負の数なので符号を変える

$=\textcolor{red}{-\sqrt{3}+2}$

【問題】 $\textcolor{green}{a=-3}$ であるとき、$\textcolor{green}{|a-2|+|a+5|}$ の値を求めなさい。

 　$|a-2|+|a+5|$

$=|-3-2|+|-2+5|$

$=|-5|+|2|$　それぞれの絶対値は

$=5+2$

$=\textcolor{red}{7}$