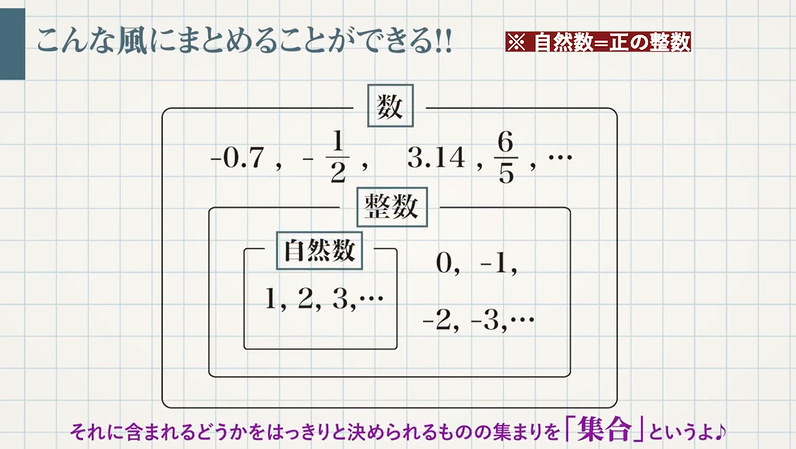
自然数全体のように、ある条件にあてはまるものをひとまとまりにして考えるとき、それを集合といいます。
整数の集合は、「自然数(正の整数)の集合」と 「$\textcolor{blue}{0}$」、「負の整数の集合」を合わせたものになります。
数の集合は、さらに範囲を広げて、「分数の形に表せる数」も含むものとなります。
関連動画
PDF教材
集合とは
集合と計算結果
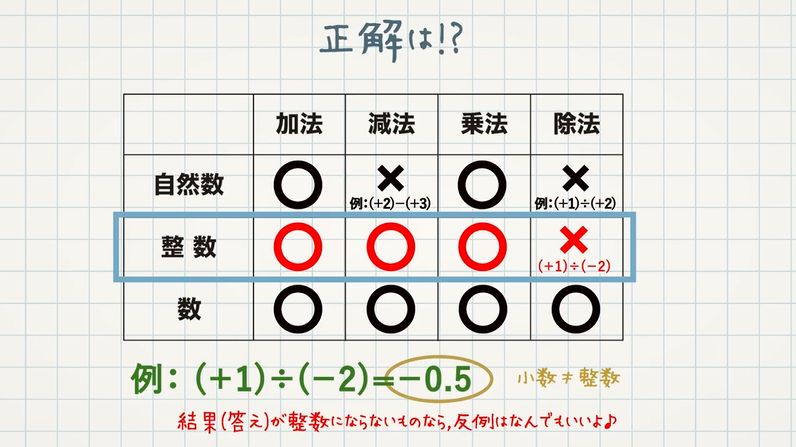
自然数の範囲の計算を考えると、和と積はいつでも自然数になります。自然数どうしの差と商は自然数にならない場合もあります。例：$(+2)-(+3)=-1$
よって、自然数の範囲では、加法と乗法はいつでもできますが、減法と除法はいつでもできるとは限りません。
整数の集合まで範囲に広げると、減法はいつでもできるようになりますが、除法はいつでもできるとは限りません。
例： $(+1)÷(-2)=-\frac{1}{2}$
よって、除法がいつでもできるようにするには数の集合まで範囲を広げて考えなければいけません。