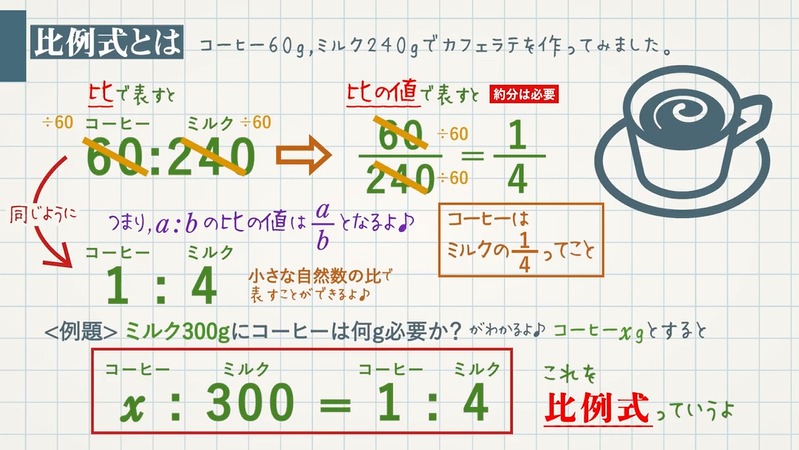
コーヒー $60\mathrm{g}$ 、ミルク $240\mathrm{g}$ でカフェラテを作ってみました。このとき、コーヒーの量とミルクの量の比を表すと、$60:240$ となります。

$$\begin{array}{rcl}& a:b& \mathrm{で}\mathrm{表}\mathrm{さ}\mathrm{れ}\mathrm{た}\mathrm{比}\mathrm{で}、a÷b\mathrm{の}\mathrm{と}\mathrm{き}\mathrm{の}\mathrm{商}（\frac{a}{b}）\mathrm{を}\end{array}$$

比の値といいます。

$60:240$ を比の値で表すと、

$$\begin{array}{r}\frac{60}{240}=\frac{1}{4} \mathrm{に}\mathrm{な}\mathrm{り}\mathrm{ま}\mathrm{す}。\end{array}$$

$a:b$ と $c:d$  の $2$ つの比の値が等しいときは、$a:b=c:d$ と表します。このように $2$ つの比が等しいことを表す式を$\mathrm{比}\mathrm{例}\mathrm{式}$といいます。

比例式の解き方はいくつかあります。

① ミルク $40\mathrm{g}$ → $300\mathrm{g}$ は $75$ 倍なので、コーヒーも $75$ 倍

　$x:300=1:4$

　　　   $x=1\times 75$

　　　   $x=75$

② 比が等しければ、比の値も等しい

　それぞれ比の値になおすと

$$\begin{array}{rcl} \frac{x}{300}& =& \frac{1}{4}\\ x& =& \frac{1}{4}\times 300\\ x& =& 75\end{array}$$

さっきの解き方よりも、一般的に比例式は

$a:b=c:d\to a\times d=b\times c$ （外$\times$外$=$内$\times$内）という「比例式の性質」を使って解きます。

$$\begin{array}{rcl} x:300& =& 1:4\\ \\ 4x& =& 300\\ \\ x& =& 75\end{array}$$

比例式の性質を使って問題を解くときのコツ

コツ①  $x$ がある方を左辺に

コツ②  かっこがある方を左辺に

【計算練習】 次の比例式を解きなさい。

$$\begin{array}{rcl}(1) 7:x& =& 49:28 \\ 49x& =& 196\\ x& =& 4\end{array}$$ $$\begin{array}{r}\\ \\ (2) x:(x-2)& =& 9:6 \\ 9(x-2)& =& 6x\\ 9x-18& =& 6x\\ 3x& =& 18\\ x& =& 6\end{array}$$