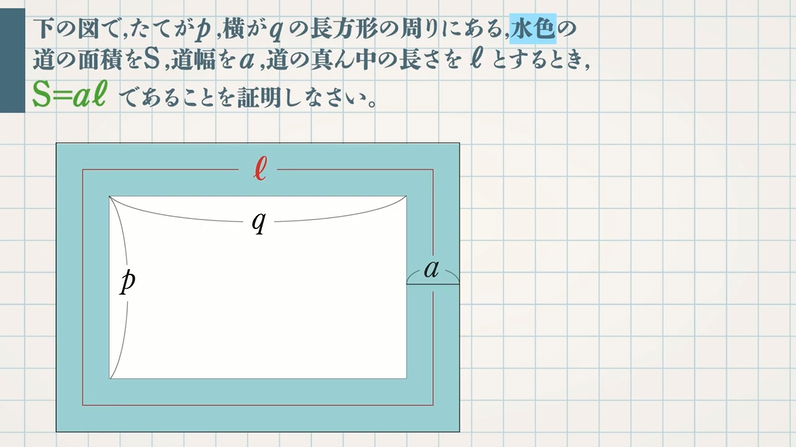
${\rm S}=aℓ$ の証明は次の $3$ つのSTEPで解くので、しっかり流れを確認しましょう。
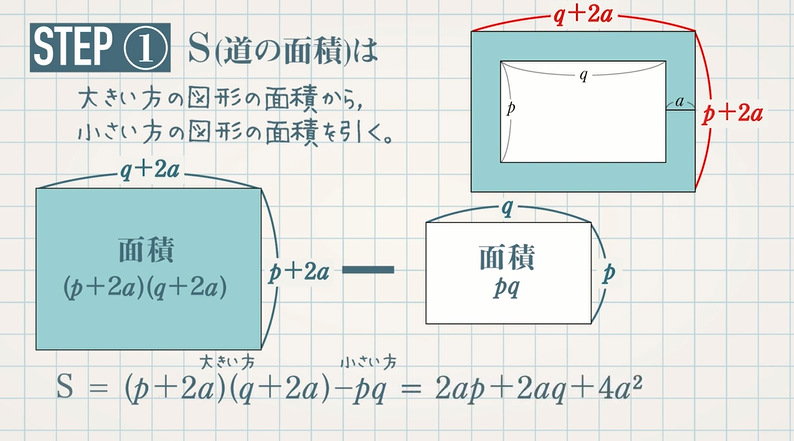
STEP①:大きい方の図形から小さい方の図形を引いて、$\textcolor{blue}{{\rm S}}$(道の面積)を $\textcolor{blue}{a,p,q}$ を用いた式で表す
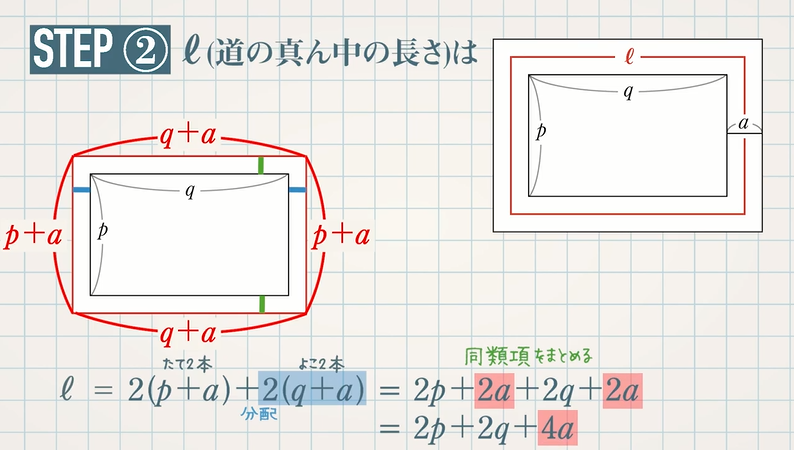
STEP②:$\textcolor{blue}{ℓ}$(道の真ん中の長さ)を $\textcolor{blue}{a,p,q}$ を用いた式で表す
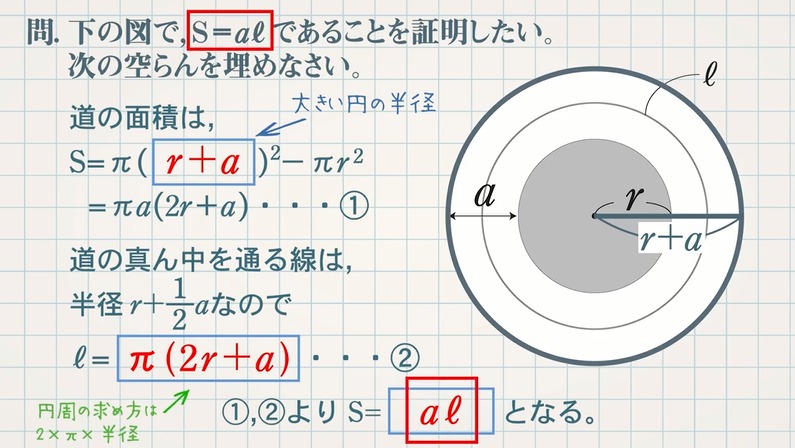
STEP③:①,②で求めた結果から $\textcolor{blue}{{\rm S}=aℓ}$ を導く