これまでに学習している数と多項式の乗法は分配法則を使って計算することができました。

\begin{eqnarray} & &\textcolor{green}{2×(3a-5)}\\ &=&2×3a+2×(-5)\\ &=&\textcolor{red}{6a-10} \end{eqnarray}

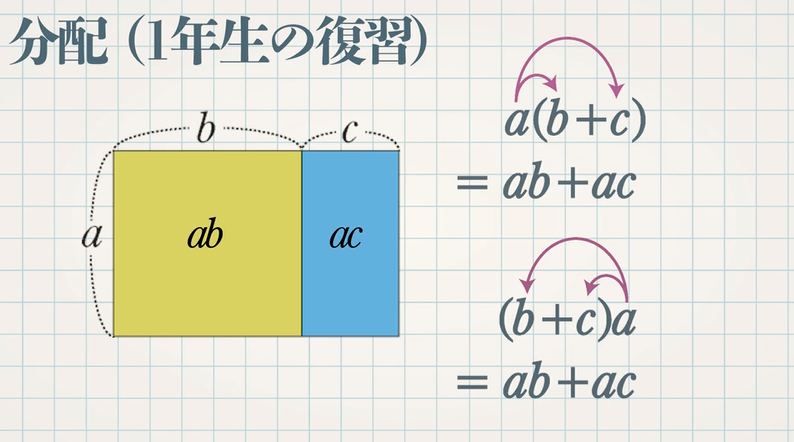
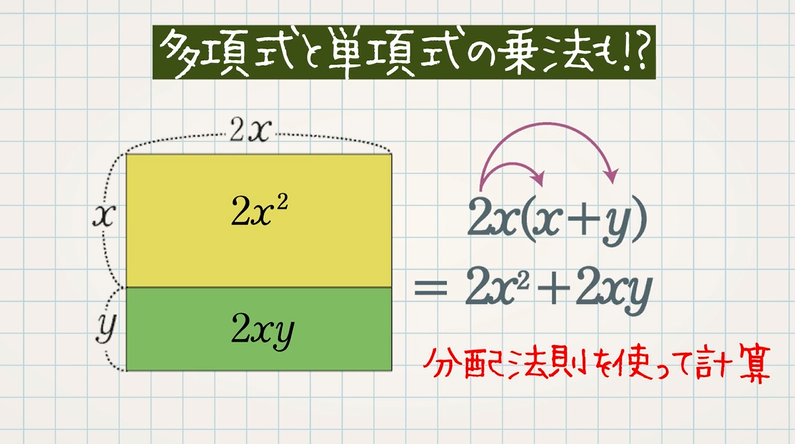
単項式と多項式の乗法も同じように分配法則を使って使って計算することができます。分配法則について確認しておきましょう。

\begin{eqnarray} a(b+c)&=&a×b+a×c=ab+ac\\ (b+c)a&=&b×a+c×a=ab+ac \end{eqnarray}

実際に単項式と多項式の乗法を分配法則を使って計算すると、次のようになります。

\begin{eqnarray} & &\textcolor{green}{2x(x+y)}\\ &=&2x×x+2x×y\\ &=&\textcolor{red}{2x^2+2xy}\\ \end{eqnarray}

\begin{eqnarray} & &\textcolor{green}{(8a-4)×(-2a)}\\ &=&8a×(-2a)-4×(-2a)\\ &=&\textcolor{red}{-16a^2+8a} \end{eqnarray}

次は多項式と単項式の除法についてです。多項式と数の除法についてはすでに学習していて、２つのアプローチ方法で計算することができました。

１.　分数になおして計算する

２.　乗法（かけ算）になおして計算する

\begin{eqnarray}\textcolor{green}{ (6a^2-8ab)÷2a}&=&\frac{6a^2}{2a}-\frac{8ab}{2a}=\textcolor{red}{3a-4b}\\ \\ \textcolor{green}{(6a^2-8ab)÷2a}&=&(6a^2-8ab)×\frac{1}{2a}=\textcolor{red}{3a-4b}\\\end{eqnarray}

わる式に分数が含まれるときは、乗法になおしてから計算します。

\begin{eqnarray} & &\textcolor{green}{(6x^2-12xy^2)÷\frac{3}{4}x}　x は上に\newline\\ &=&(6x^2-12xy^2)÷\frac{3x}{4}　\textcolor{blue}{÷を×に(逆数)}\newline\\\ &=&(6x^2-12xy^2)\textcolor{blue}{×\frac{4}{3x}}　分配\newline\\\ &=&6x^2y×\frac{4}{3x}-12xy^2×\frac{4}{3x}\newline\\\ &=&\textcolor{red}{8x-16y^2} \end{eqnarray}