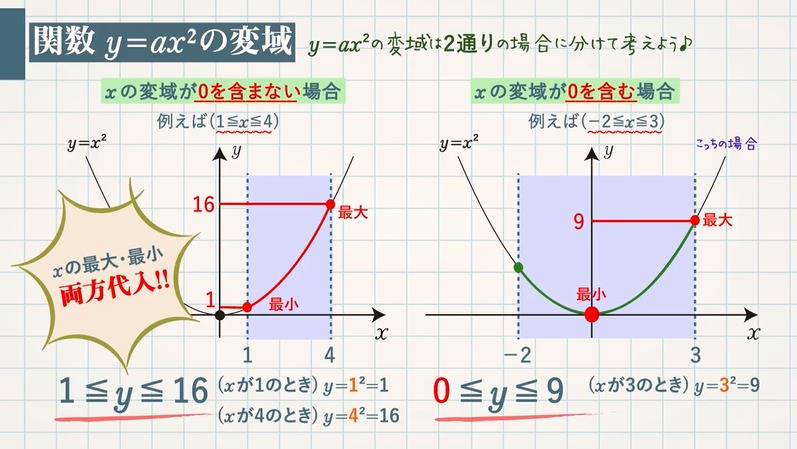
$\textcolor{green}{y=ax^2}$ の変域は、$\textcolor{green}{x}$ の変域が $\textcolor{green}{0}$ を含む場合と含まない場合の $\textcolor{green}{2}$ 通りに分けて考えます。$\textcolor{green}{y=x^2}$ で確認しましょう。

$\textcolor{green}{x}$ の変域が $\textcolor{green}{0}$ を含まない場合（$\textcolor{green}{1≦x≦4}$ ）

$x$ の変域を両方代入して最大、最小を求める

（$x=1$ のとき）　$y=\textcolor{blue}{1}^2=\textcolor{blue}{1}$

（$x=4$ のとき）　$y=\textcolor{blue}{4}^2=\textcolor{blue}{16}$

よって、$\textcolor{red}{1≦y≦16}$

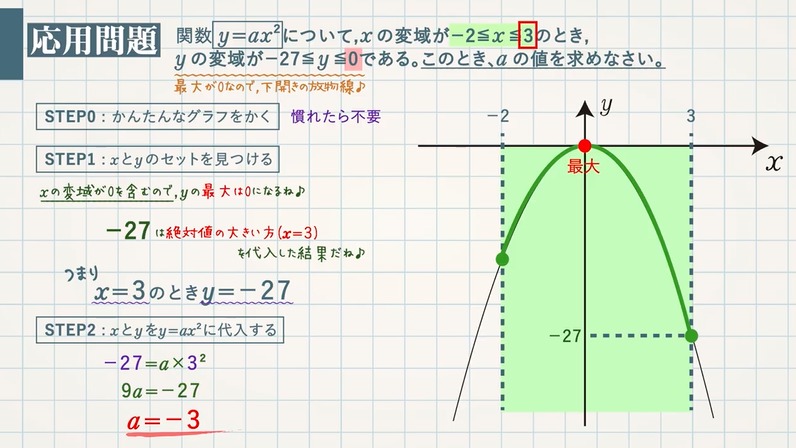
$\textcolor{green}{x}$ の変域が $\textcolor{green}{0}$ を含む場合（ $\textcolor{green}{-2≦x≦3}$）

上に開くグラフなので、その最小は $\textcolor{blue}{0}$

最大は、絶対値の大きい方を式に代入して求める。

（$x=3$ を代入）　$y=\textcolor{blue}{3}^2=\textcolor{blue}{9}$

よって、$\textcolor{red}{0≦y≦9}$

【基本問題】関数 $\textcolor{green}{y=-2x^2}$ について、$\textcolor{green}{x}$ の変域が次のようなとき、$\textcolor{green}{y}$ の変域を求めなさい。

(1) $\textcolor{green}{1≦x≦2}$　（$\textcolor{blue}{x}$ の変域に $\textcolor{blue}{0}$ を含まない）

→両方代入

$y=-2×1^2=\textcolor{blue}{-2}　（最大）$

$y=-2×2^2=\textcolor{blue}{-8}　（最小）$　　

よって、$\textcolor{red}{-8≦y≦-2}$

(2) $\textcolor{green}{-5＜x＜3}$　（$\textcolor{blue}{x}$ の変域に $\textcolor{blue}{0}$ を含む）

→片方は $\textcolor{blue}{0}$。絶対値の大きい方を代入

$y=-2×(-5)^2=\textcolor{blue}{-50}　（最小）$　

よって、$\textcolor{red}{-50≦y≦0}$

(3) $\textcolor{green}{-4＜x≦-2}$　（$\textcolor{blue}{x}$ の変域に $\textcolor{blue}{0}$ を含まない）

→両方代入

$y=-2×(-4)^2=\textcolor{blue}{-32}　（最小）$

$y=-2×(-4)^2=\textcolor{blue}{-8}$　   $（最大）$　　

よって、$\textcolor{red}{-32＜y≦-8}$

【応用問題】関数 $\textcolor{green}{y=ax^2}$ について、$\textcolor{green}{x}$ の変域が $\textcolor{green}{-2≦x≦3}$ のとき、$\textcolor{green}{y}$ の変域が $\textcolor{green}{-27≦y≦0}$ である。このとき、$\textcolor{green}{a}$ の値を求めなさい。

STEP $\textcolor{blue}{0}$：かんたんなグラフを書く　※慣れたら不要

$-27≦y≦0$ より、最大が $\textcolor{blue}{0}$ なので、下開きの放物線になります。

STEP $\textcolor{blue}{1}$：$\textcolor{blue}{x}$ と $\textcolor{blue}{y}$ のセットを見つける

$x$ の変域が $0$ を含むので、$y$ の最大は $\textcolor{blue}{0}$ 。$-27$ は絶対値の大きい方（$\textcolor{blue}{x=3}$）を代入した結果となります。つまり、$x=3$ のとき $y=-27$ となります。

STEP $\textcolor{blue}{2}$：$\textcolor{blue}{x}$ と $\textcolor{blue}{y}$ を $\textcolor{blue}{y=ax^2}$ に代入する

\begin{eqnarray}　　　 -27&=&a×3^2\\ 9a&=&-27\\ \textcolor{red}{a}&\textcolor{red}{=}&\textcolor{red}{-3} \end{eqnarray}