規則性に関する問題－２次方程式：中学３年生

今回は, 規則性に関するタイプの問題をみていきましょう。

規則性に関する問題

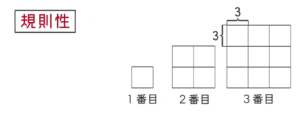
図のように, １辺が $\rm 3cm$ の正方形を並べて図形をつくるとき, 次の問いに答えなさい。

規則性の問題は２次方程式の範囲だとわかっていると, 本当に簡単です。難しい問題以外は規則といっても $\rm n^2$ や $\rm ～n^2$ , もしくは $\rm (n±〇)^2$ ぐらいしか選択肢がないので, そこまで迷わないかなと思います。

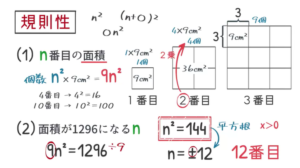
$(1)$ $\rm n$ 番目の図形の面積を $\rm n$ を用いて表しなさい。

図形の“個数”に着目しましょう。１番目なら正方形は１個,２番目なら４個,３番目なら９個・・・。ここから“個数”は〇番目の２乗になっていることがわかります。

よって, $\rm n$ 番目なら $\rm n^2$ 個。ただ, 今回は $\rm n$ 番目の面積なので, そこを考えないといけません。

正方形１個あたりの面積は $\textcolor{blue}{\rm 3cm×3cm=9cm^2}$。この $9$ と“個数”をかければ全体の面積を求めることができます。

例えば正方形が１個なら $\textcolor{blue}{\rm 1×9=9cm^2}$。４個だったら$\textcolor{blue}{\rm 4×9=36cm^2}$ みたいな感じですかね。

よって, $\rm n^2$ 個に $9$ をかけて, $\rm n^2×9=\textcolor{red}{9n^2}$。これが $(1)$ の答えになります。

$(2)$ 面積が $\rm 1296cm^2$ になるのは, 何番目の図形か。

これは $(1)$ で作った面積の式 $\textcolor{blue}{\rm 9n^2=1296}$ として方程式を作り, 解けばＯＫです。

平方根の考えを利用した解き方ですね。まずは「$\rm n^2=$」の形を作りましょう。

両辺を $9$ で割って, $\textcolor{blue}{\rm n^2=144}$。

「$\rm n^2=$」の形ができたら, 左辺は２乗を外して $\rm n$ , 右辺には平方根を書く。$144$ の平方根なんで $\textcolor{blue}{\rm n=±12}$ 。

ただし, 何番目かを聞かれているので負の数はＮＧ。答えは１２番目になります。

今回は規則性に関する問題でした。

解説動画はコチラ ↓

各PDFはコチラ↓
問題
https://ecommons.biz/wp-content/uploads/2021/10/R17-3-01-1.pdf
解答欄
https://ecommons.biz/wp-content/uploads/2021/10/R17-3-01-2.pdf
解答
https://ecommons.biz/wp-content/uploads/2021/10/R17-3-01-3.pdf

関連記事はコチラ↓
解と定数に関する問題
https://ic0.tv/press/r17-1-6/
道幅に関する問題
https://ic0.tv/press/r17-1-7/
立体の容積に関する問題
https://ic0.tv/press/r17-1-8/
面積に関する問題
https://ic0.tv/press/r17-1-9/
動く点に関する問題
https://ic0.tv/press/r17-1-11/
数に関する問題
https://ic0.tv/press/r17-1-12/
座標平面に関する問題
https://ic0.tv/press/r17-1-9/