動く点に関する問題-2次方程式:中学3年生
今回は2次方程式の応用の中でも動く点に関する問題をみていこうと思います。
動く点(四角形)
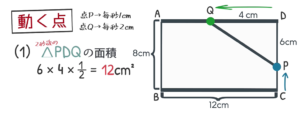 大問1:図のように縦 $\rm 8cm$ , 横 $\rm 12cm$ の長方形$\rm ABCD$ がある。点 $\rm P,Q$ はそれぞれ点 $\rm C,D$ を同時に出発し, 点 $\rm P$ は毎秒 $\rm 1cm$ の速さで辺$\rm CD$ 上を $\rm D$ まで, 点 $\rm D$ は毎秒 $\rm 2cm$ の速さで辺 $\rm AD$ 上を $\rm A$ まで, 矢印の方向に移動するとき, 次の問いに答えなさい。
大問1:図のように縦 $\rm 8cm$ , 横 $\rm 12cm$ の長方形$\rm ABCD$ がある。点 $\rm P,Q$ はそれぞれ点 $\rm C,D$ を同時に出発し, 点 $\rm P$ は毎秒 $\rm 1cm$ の速さで辺$\rm CD$ 上を $\rm D$ まで, 点 $\rm D$ は毎秒 $\rm 2cm$ の速さで辺 $\rm AD$ 上を $\rm A$ まで, 矢印の方向に移動するとき, 次の問いに答えなさい。
動点の問題で一番大切なのは, 点が動いてきた“距離・長さ”をしっかりと把握することです。今回だと点 $\rm P$ が毎秒 $\rm 1cm$ で $\rm C$ から $\rm D$ に, 点 $\rm Q$ が毎秒 $\rm 2cm$ で $\rm D$ から $\rm A$ へ動きます。このときの $\rm DP,DQ$ の長さが重要です。
$(1)$ 出発してから2秒後 $\rm △PDQ$ の面積を求めなさい。
$(1)$ のように, 方程式と関係ない問題が初めに入っていることもあります。
点 $\rm P$ は毎秒 $\rm 1cm$ なので $\rm 2cm$ 進む, 残った部分 $\textcolor{blue}{\rm DP=8-2=6cm}$
点 $\rm Q$ は毎秒$\rm 2cm$ なので $\rm 4cm$ 進む, よって $\textcolor{blue}{\rm DQ=4cm}$
三角形の面積なので, 底辺×高さ×$\frac{1}{2}$。よって, $6×4×\frac{1}{2}=\textcolor{red}{\rm 12cm^2}$
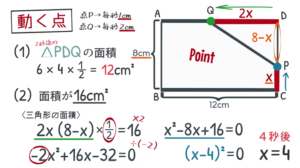
$(2)$ $\rm △PDQ$ の面積が $\rm 16 cm^2$ になるのは出発してから何秒後ですか。
まずは, 動いた部分を $\rm x$ を使って表していきましょう。
点 $\rm P$ は毎秒 $\rm 1cm$ なので, 移動距離は $\rm 1×x=xcm$
点 $\rm Q$ は毎秒 $\rm 2cm$ なので, 移動距離は $\rm2×x=2xcm$
よって, $\rm DQ$ の長さはそのまま $\rm 2x$
$\rm DP$ は全体 $\rm 8cm$ から$\rm CP$ の長さ $\rm xcm$を引いた $\rm 8-x$
面積が $16$ なので, $\textcolor{blue}{\rm 2x(8-x)×\frac{1}{2}=16}$。
今回は $2$ を全体にかけて分数を消しましょう。$\textcolor{blue}{\rm -2x^2+16x-32=0}$
次に, $x^2$ の前に数字がついているので, 全体を $-2$ で割る。$\textcolor{blue}{\rm x^2-8x+16=0}$
あとはいつも通り, 左辺を因数分解。$\textcolor{blue}{\rm (x-4)^2=0}$。よって $\textcolor{blue}{\rm x=4}$
“4秒後” が答えになります。
動く点(三角形)
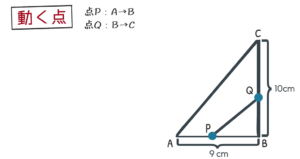 図のような直角三角形 $\rm ABC$ で, 点 $\rm P$ は $\rm A$ を出発して辺 $\rm AB$ 上を $\rm B$ まで動く。また, 点 $\rm Q$ は点 $\rm P$ が $\rm A$ を出発するのと同時に $\rm B$ を出発し, 点 $\rm P$ と同じ速さで辺 $\rm BC$ 上を $\rm C$ まで動く。点 $\rm P$ が $\rm A$ から動いた長さを $\rm xcm$ とする。点 $\rm P$ が $\rm A$ から何 $\rm cm$ 動いたとき $\rm △PBQ$ の面積が $\rm 9 cm^2$ になりますか。
図のような直角三角形 $\rm ABC$ で, 点 $\rm P$ は $\rm A$ を出発して辺 $\rm AB$ 上を $\rm B$ まで動く。また, 点 $\rm Q$ は点 $\rm P$ が $\rm A$ を出発するのと同時に $\rm B$ を出発し, 点 $\rm P$ と同じ速さで辺 $\rm BC$ 上を $\rm C$ まで動く。点 $\rm P$ が $\rm A$ から動いた長さを $\rm xcm$ とする。点 $\rm P$ が $\rm A$ から何 $\rm cm$ 動いたとき $\rm △PBQ$ の面積が $\rm 9 cm^2$ になりますか。
三角形に変わっただけで, 基本的な解き方は先程と同じです。違いは, 今回は $\rm x$ 秒後という時間ではなく, $\rm xcm$ と“長さ”が直接 $\rm x$ となっている点です。
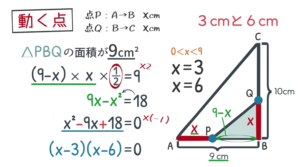
$\rm △PBQ$ の面積が $9$ のときの $\rm x$ を求めるので, $\rm BP$ と $\rm BQ$ を $\rm x$ を使って表します。
$\rm BQ$ はそのまま $\rm x$ , $\rm BP$ は全体 $\rm 9cm$ から $\rm x$ を引くので, $\rm 9-x$ と表すことができます。
その面積は, $\textcolor{blue}{\rm x×(9-x)×\frac{1}{2}=9}$
分数を消すために全体を $2$ 倍して分配, 右辺の $18$ を移項すると, $\textcolor{blue}{\rm -x^2+9x-18=0}$
先頭にマイナスがあるので, 全体を“$×(-1)$”すると, $\textcolor{blue}{\rm x^2-9x+18=0}$
左辺を因数分解して, $\textcolor{blue}{\rm (x-3)(x-6)=0}$。よって, $x=3,6$
今回はどちらも問題に合っているので, 答えは $\textcolor{red}{\rm 3cm, 6cm}$
動く点(2つの正方形)
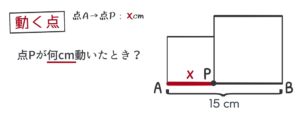 長さ $\rm 15cm$ の線分 $\rm AB$ がある。点 $\rm P$ は $\rm A$ を出発して $\rm B$ まで動く。このとき, $\rm AP, PB$ をそれぞれ1辺とする2つの正方形の面積の和が $\rm 113cm^2$ になるのは, 点 $\rm P$ が何 $\rm cm$ 動いたときか求めなさい。
長さ $\rm 15cm$ の線分 $\rm AB$ がある。点 $\rm P$ は $\rm A$ を出発して $\rm B$ まで動く。このとき, $\rm AP, PB$ をそれぞれ1辺とする2つの正方形の面積の和が $\rm 113cm^2$ になるのは, 点 $\rm P$ が何 $\rm cm$ 動いたときか求めなさい。
これは珍しいタイプの問題で, 点 $\rm P$ が移動する $\rm AP,PB$ を1辺とする正方形2つの面積がわかっていて, 移動した距離 $\rm x cm$ を求めるものになります。
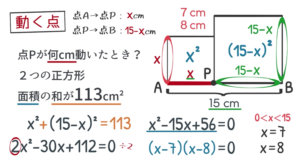
ここも“速さ”ではなく動いた距離が $\rm xcm$ なので, $\rm P$ が通った $\rm AP$ 間を $\rm x$。残りの $\rm PB$ 間を $\rm 15-x$ と表すことができます。
どちらも正方形なので, 縦の長さは横の長さと同じ $\rm x$ と $\rm 15-x$ となります。
面積の和が $113$ なので, 式は $\textcolor{blue}{\rm x^2+(15-x)^2=113}$
左辺を展開して, 右辺の $113$ を移項して整理すると, $\textcolor{blue}{\rm 2x^2-30x+112=0}$
$x^2$ の係数 $2$ で全体を割ると, $\textcolor{blue}{\rm 2x^2-30x+112=0}$
左辺を因数分解して, $\textcolor{blue}{\rm (x-7)(x-8)=0}$。よって, $\textcolor{blue}{\rm x=7,8}$
$\rm AB$ 間は $\rm 15cm$ なので, どちらも問題に合っています。よって, 答えは $\textcolor{red}{\rm 7cm,8cm}$
今回は動く点に関する問題でした。
各PDFはコチラ↓
問題
https://ecommons.biz/wp-content/uploads/2021/10/R17-4-01-1.pdf
解答欄
https://ecommons.biz/wp-content/uploads/2021/10/R17-4-01-2.pdf
解答
https://ecommons.biz/wp-content/uploads/2021/10/R17-4-01-3.pdf
関連記事はコチラ↓
解と定数に関する問題
https://ic0.tv/press/r17-1-6/
道幅に関する問題
https://ic0.tv/press/r17-1-7/
立体の容積に関する問題
https://ic0.tv/press/r17-1-8/
面積に関する問題
https://ic0.tv/press/r17-1-9/
規則性に関する問題
https://ic0.tv/press/r17-1-10/
数に関する問題
https://ic0.tv/press/r17-1-12/
座標平面に関する問題
https://ic0.tv/press/r17-1-9/
デジタル板書データはコチラ↓
2次方程式の利用②動点
https://ic0.tv/class/mathematics/middle-school/016/nijihoteishiki-insubunkai/