座標平面に関する問題－２次方程式：中学３年生

今回は座標平面に関する問題についてみていきましょう。

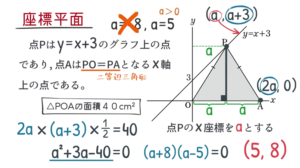図で点 $\rm P$ は $\rm y=x+3$ のグラフ上の点であり, 点 $\rm A$ は $\rm PO=PA$ となる $\rm x$ 軸上の点である。点 $\rm P$ の $\rm x$ 座標を $\rm a$ として, 次の座標を求めなさい。ただし, $\rm a>0$ とします。

$(1)$ 点$ \rm P$ の $\rm y$ 座標

これはシンプルに１次関数 $\rm y=x+3$ の $\rm x$ に $\rm a$ に代入してあげればOKです。

答えは, $\textcolor{red}{\rm a+3}$

$(2)$ 点$ \rm A$ の座標

ポイントは「二等辺三角形」ということ。二等辺三角形の頂角の二等分線は底辺を垂直に $2$ 等分します。

頂点 $\rm P$ から底辺に垂線を引くと, 底辺 $\rm (AO)$ をちょうど半分にするということですね。

点 $\rm P$ の $\rm x$ 座標が $\rm a$ なので, $\rm y$ 軸からの距離が $\rm a$ になる。これが底辺の中点になるので, 右サイドも $\rm a$。

よって, 点 $\rm A$ の $\rm x$ 座標は, $\textcolor{blue}{\rm a+a=2a}$

$\rm y$ 座標は $0$ なので, $\textcolor{red}{\rm A(2a,0)}$

$(3)$ 座標の $1$ 目もりを $\rm 1cm$ として, $\rm △POA$ の面積が $\rm 40cm^2$ になるときの点 $\rm P$ の座標

ここまでが前提で, ここが一番聞きたいところです。必要な値は, ここまでの問いで得られています。

あとは面積の公式にしたがって式を作るだけですね。

底辺 $\rm (OA)$ は $\textcolor{blue}{\rm 2a}$ , 高さは点 $\rm P$ の $\rm y$ 座標なので, $\textcolor{blue}{\rm a+3}$ になる。

三角形の面積の式に表すと, $\textcolor{blue}{\rm 2a×(a+3)×\frac{1}{2}=40}$

式を整理すると, $\textcolor{blue}{\rm a^2+3a-40=0}$

左辺を因数分解すると, $\textcolor{blue}{\rm (a+8)(a-5)=0}$

$\rm a=-8,5$ ですが, 問題文に $\rm a>0$ と書いてあるので, $\textcolor{blue}{\rm a=5}$

点 $\rm P$ の座標なので, $\rm P(a,a+3)$ に $\rm a$ に $5$ を代入する。

よって, 答えは $\textcolor{red}{\rm P(5,8)}$

今回は座標平面に関する問題でした。

各PDFはコチラ↓
問題
https://ecommons.biz/wp-content/uploads/2021/10/R17-4-01-1.pdf
解答欄
https://ecommons.biz/wp-content/uploads/2021/10/R17-4-01-2.pdf
解答
https://ecommons.biz/wp-content/uploads/2021/10/R17-4-01-3.pdf

関連記事はコチラ↓
解と定数に関する問題
https://ic0.tv/press/r17-1-6/
道幅に関する問題
https://ic0.tv/press/r17-1-7/
立体の容積に関する問題
https://ic0.tv/press/r17-1-8/
面積に関する問題
https://ic0.tv/press/r17-1-9/
規則性に関する問題
https://ic0.tv/press/r17-1-10/
動く点に関する問題
https://ic0.tv/press/r17-1-11/
数に関する問題
https://ic0.tv/press/r17-1-12/