面積に関する問題-2次方程式:中学3年生
今回は, 面積に関するタイプの問題をみていきましょう。
面積に関する問題
 1辺 $\rm x cm$ の正方形の縦を $\rm 3cm$ 短くし, 横を $\rm 2cm$ 長くして長方形をつくると, 長方形の面積は $\rm 50 cm^2$ になった。もとの正方形の1辺の長さを求めなさい。
1辺 $\rm x cm$ の正方形の縦を $\rm 3cm$ 短くし, 横を $\rm 2cm$ 長くして長方形をつくると, 長方形の面積は $\rm 50 cm^2$ になった。もとの正方形の1辺の長さを求めなさい。
他の図形に関する問題よりはやや簡単かなと思います。問題文にある通り辺の長さを変えると, 下のような長方形ができます。
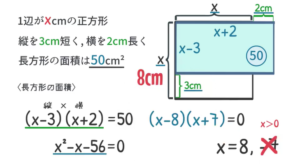 あとは縦, 横の長さを $\rm x$ を使って表し, 長方形の面積を求める式を作るだけになります。
あとは縦, 横の長さを $\rm x$ を使って表し, 長方形の面積を求める式を作るだけになります。
縦は $\rm x$ を $\rm 3cm$ 短くしたので, $\textcolor{blue}{\rm x-3}$。横は $\rm x$ を $\rm 2cm$ 長くしたので, $\textcolor{blue}{\rm x+2}$。その面積が $50$ なので, $\textcolor{blue}{\rm (x-3)(x+2)=50}$
左辺を展開, 右辺の $50$ を移項すると, $\textcolor{blue}{\rm x^2-x-56=0}$。
左辺を因数分解して, $\textcolor{blue}{\rm (x-8)(x+7)=0}$。$\textcolor{blue}{\rm x=8,-7}$
図形で負の数はNGなんで, 答えは $\textcolor{red}{\rm 8cm}$ となります。
今回は, 面積に関するタイプの問題でした。
解説動画はコチラ ↓
各PDFはコチラ↓
問題
https://ecommons.biz/wp-content/uploads/2021/10/R17-3-01-1.pdf
解答欄
https://ecommons.biz/wp-content/uploads/2021/10/R17-3-01-2.pdf
解答
https://ecommons.biz/wp-content/uploads/2021/10/R17-3-01-3.pdf
関連記事はコチラ↓
解と定数に関する問題
https://ic0.tv/press/r17-1-6/
道幅に関する問題
https://ic0.tv/press/r17-1-7/
立体の容積に関する問題
https://ic0.tv/press/r17-1-8/
規則性に関する問題
https://ic0.tv/press/r17-1-10/
動く点に関する問題
https://ic0.tv/press/r17-1-11/
数に関する問題
https://ic0.tv/press/r17-1-12/
座標平面に関する問題
https://ic0.tv/press/r17-1-9/
デジタル板書データはコチラ↓
2次方程式の利用①図形系
https://ic0.tv/class/mathematics/middle-school/016/nijihoteishiki-insubunkai/