小学校までの数の範囲は $0$ より大きい数だけでしたが、中学校からは範囲を広げて、$0$ より小さい数についても考えてみましょう。

$0$ を基準として $0$ より $5$ 大きい数を $\textcolor{blue}{+5}$ と表すと、$0$ より $5$ 小さい数は $\textcolor{blue}{-5}$ と表すことができ、$0$ より大きい数を正の数、 $0$ より小さい数を負の数といいました。※ $\textcolor{blue}{0}$ は正の数でも負の数でもありません。

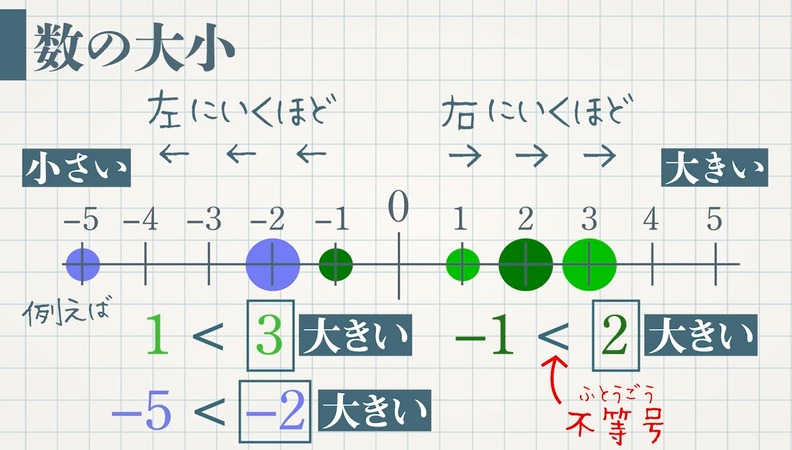
これらの数を数直線上の点で表すことについて考えましょう。

負の数は数直線を $\textcolor{blue}{0}$ より左へのばした直線上に表すことができます。数直線で $0$ を表す点を原点といい、数直線の右の方向を正の向き、左の方向を負の向きといいます。

数の大小について数直線を使って考えてみましょう。

数直線上では、右側にある数ほど（正の方向へ進むほど）大きく、左側にある数ほど（負の方向へ進むほど）小さくなります。

例えば、次の $2$ 数の大小を比べると

　　$1$　 と 　 $3$ 　　　$\textcolor{blue}{1<3}$

　$-1$　 と 　 $2$ 　　$\textcolor{blue}{-1<2}$

　$-5$　 と   $-2$　　 $\textcolor{blue}{-5<-2}$

このように数の大小は不等号を使って表すことができ、不等号の向きは $2$ つになります。

小さい　＜　大きい　 ＜ ←読み方は「しょうなり」

大きい　＞　小さい　 ＞ ←読み方は「だいなり」

【問題】次の $\textcolor{green}{3}$ つの数の大小を、不等号を使い表しなさい。

　$\textcolor{green}{-1　,　-5　,　2}$

$3$ つの数字の大小関係を不等号で表す場合、下のように表してはいけないことに注意が必要です。

$-1＞-5＜2$　←$\textcolor{blue}{-1}$ と $\textcolor{blue}{2}$ どちらが大きいかわからない

よって、答えは $\textcolor{red}{-5＜-1＜2}$  ($\textcolor{red}{2＞-1＞-5}$) 

数直線上で、ある数を表す点と $\textcolor{blue}{0}$ (原点)との距離を絶対値といいます。

例えば、絶対値が $4$ である数(原点からの距離が $4$ である数)は $\textcolor{blue}{+4}$ と $\textcolor{blue}{-4}$ の $\textcolor{blue}{2}$ つがあります。

ちなみに、$\textcolor{blue}{0}$ の絶対値は $\textcolor{blue}{0}$ になります。

$-5$ と $+3$ の $2$ 数について、$-5$ の方が数としては小さくなりますが、絶対値は大きくなります。

$-5$ の絶対値：$\textcolor{blue}{5}$　　$+3$ の絶対値：$\textcolor{blue}{3}$