PDF教材

ダウンロード

たし算のことを加法といい、加法の結果を和といいます。

まずは同じ符号の $\textcolor{blue}{2}$ 数の加法について考えましょう。

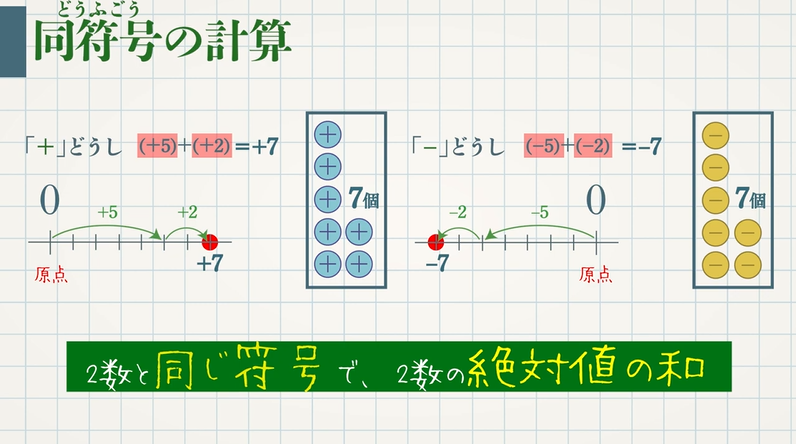
正の数どうしの $(+5)+(+2)$ を数直線で考えると、$0$ から正の方向へ $5$ 進み、さらに正の方向へ $2$ 進むので、結果として正の方向へ $\textcolor{blue}{7}$ 進んだことになります。($\textcolor{blue}{+}$ が $\textcolor{blue}{7}$ 個)

よって、$(+5)+(+2)=\textcolor{blue}{+7}$

負の数どうしの $(-5)＋(-2)$ を数直線で考えると、$0$ から負の方向へ $5$ 進み、さらに負の方向へ $2$ 進むので、結果として負の方向へ $\textcolor{blue}{7}$ 進んだことになります。($\textcolor{blue}{-}$ が $\textcolor{blue}{7}$ 個)

よって、$(-5)+(-2)=\textcolor{blue}{-7}$

同じ符号の $2$ 数の和は、

符号：$\textcolor{blue}{2}$ 数と同じ符号　絶対値：$\textcolor{blue}{2}$ 数の絶対値の和　となります。

異なる符号の $2$ 数の加法で、絶対値が等しい $\textcolor{blue}{2}$ 数の和はどうなるか考えましょう。

$(+4)+(-4)$ を数直線で考えると、$0$ から正の方向へ $4$ 進み、次に負の方向へ $4$ 進むので、結果として $\textcolor{blue}{0}$ (原点) にもどることになります。

よって、$(+4)+(-4)=\textcolor{blue}{0}$

絶対値が等しく、符号が異なる $2$ 数の和は、$\textcolor{blue}{0}$ になります。

続いては異なる符号の $\textcolor{blue}{2}$ 数の加法について考えましょう。

$(+5)+(-2)$ を数直線で考えると、$0$ から正の方向へ $5$ 進み、次に負の方向に $2$ 進むので、結果として正の方向へ $\textcolor{blue}{3}$ 進んだことになります。($\textcolor{blue}{+}$ が $\textcolor{blue}{3}$ 個)

よって、$(+5)+(-2)=\textcolor{blue}{+3}$

$(-5)+(+2)$ を数直線で考えると、$0$ から負の方向へ $5$ 進み、次に正の方向へ $2$ 進むので、結果として負の方向へ $\textcolor{blue}{3}$ 進んだことになります。($\textcolor{blue}{-}$ が $\textcolor{blue}{3}$ 個)

よって、$(-5)+(+2)=\textcolor{blue}{-3}$

異なる符号の $2$ 数の和は、

符号：絶対値の大きい方の符号　絶対値：絶対値の大きい方から小さい方をひいた差　となります。