ひき算のことを減法といい、その計算結果を差といいます。

正の数、負の数どちらをひく計算であっても、おさえるポイントは $1$ つだけです。

ポイント：ひく数の符号を変えて、加法になおしてから計算する。

$(+3)-(+2) → (+3)\textcolor{blue}{+}(\textcolor{blue}{-}2)=+1$

$(+3)-(-2) → (+3)\textcolor{blue}{+}(\textcolor{blue}{+}2)=+5$

【問題】答えが $\textcolor{green}{+3}$ になる式を $\textcolor{green}{1}$ つ選びなさい。

　A.　$\textcolor{green}{(+2)-(+1)}$

　B.　$\textcolor{green}{(-1)-(-2)}$

　C.　$\textcolor{green}{(+2)-(-1)}$

　D.　$\textcolor{green}{(-1)-(+2)}$

それぞれのひく数の符号を変えて、加法の式になおすと、

　A.　$(+2)\textcolor{blue}{+}(\textcolor{blue}{-}1)=+1$

　B.　$(-1)\textcolor{blue}{+}(\textcolor{blue}{+}2)=+1$

　C.　$(+2)\textcolor{blue}{+}(\textcolor{blue}{+}1)=\textcolor{red}{+3}$

　D.　$(-1)\textcolor{blue}{+}(\textcolor{blue}{-}2)=-3$

よって、答えは C

加法と減法が混じった式の計算のしかたを考えましょう。減法は加法になおすことができるので、加法と減法の混じった式は、加法だけの式になおして計算します。

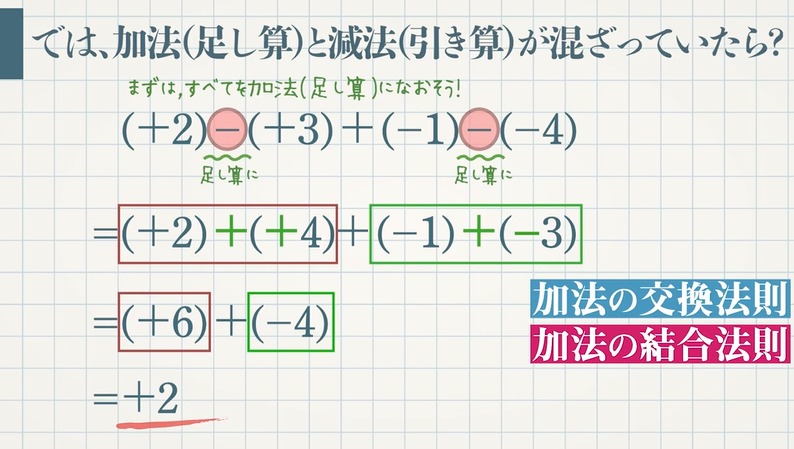
【問題】次の計算をしなさい。

　$\textcolor{green}{(+2)-(+3)+(-1)-(-4)}$　　加法になおす

$=(+2)\textcolor{blue}{+}(\textcolor{blue}{-}3)+(-1)\textcolor{blue}{+}(\textcolor{blue}{+}4)$　　加法の交換法則

$=(+2)\textcolor{blue}{+}(+4)+(-1)\textcolor{blue}{+}(-3)$　　加法の結合法則

$=(+6)+(-4)$

$=\textcolor{red}{+2}$

加法だけの式のそれぞれの数のことを項といいます。また、正の数の項を正の項、負の数の項を負の項といいます。

$(+2)+(-3)+(-1)+(+4)$　

項：$\textcolor{blue}{+2,-3,-1,+4}$　（正の項：$\textcolor{blue}{+2,+4}$　負の項：$\textcolor{blue}{-3,-1}$）

加法だけの式では、符号＋とかっこを省いた項だけを並べた式に変えることができます。また、式のはじめの項が正の数のときは、符号＋を省くこともあります。

　 $2-3-1+4$

$=2+4-1-3$

$=6-4$

$=\textcolor{blue}{2}$

項だけを並べた式では、加法の交換法則,結合法則を使うことができます。

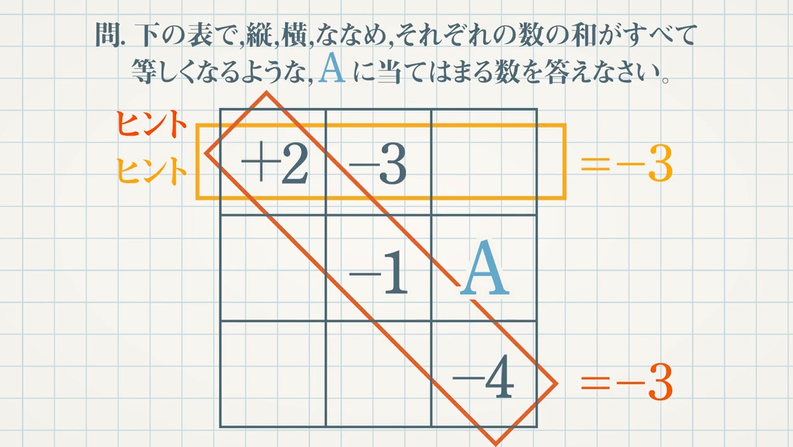
【問題】表で縦,横,ななめのそれぞれの数の和がすべて等しくなるような $\textcolor{green}{\rm A}$ に当てはまる数を答えなさい。

ななめラインの $3$ 数($+2,-1,-4$)がわかっているので、和を計算します。$2-1-4=\textcolor{blue}{-3}$

次に上段ラインの $2$ 数があり、和が $\textcolor{blue}{-3}$ になればよいので、

$2-3+〇=\textcolor{blue}{-3}$　よって、$\textcolor{blue}{-2}$

これにより、右段の縦ラインの $2$ 数がわかったので、

$-2+〇-4=\textcolor{blue}{-3}$　よって、$\rm A=\textcolor{red}{+3}$