平方完成を使った解き方－２次方程式：中学３年生

今回は, 平方完成を使った解き方についてみていきましょう。

平方完成とは

まず「平方完成」と言ってもほとんどの人がわからないと思います。教科書には多分載っていなくて, 高校の範囲ですかね？「平方完成」は２次方程式だけでなく他の単元でも使えるので, とりあえず基礎だけ先にやっておきます。

「平方完成」では $\rm (　　)^2$ って形を作ります。今日は最もシンプルなタイプの $\rm x^2$ の係数が $\rm 1$ で $\rm x$ の係数が偶数ってタイプを説明していこうと思います。高校へ行くともう少し難しいのも出るんですが, “２次方程式”の問題と考えると, ここだけ理解したら十分です。

教科書には分数になるタイプも入ってますが, あまり“負担”が変わんないんで「解の公式」で解ければ十分かと思います。

やり方としては $\rm x$ の係数（$\rm 2a$）の半分の数字を使って２乗の形を作ってしまう。何も変えない $\rm b$ はそのままですね。

「展開」習っているので分かると思うんですけど, 展開しても上の式と同じ形にならない。今回でいうと $\rm x^2+2ax$ っていうところが同じなんですが, $\rm a^2$ っていう余分なものが付いてきたんですね。そこで上の式と同じ値にする為に, 余分な $\rm a^2$ を引いてあげる。これで“上下”の式が同じ値になります。

実際 $\rm a$ や $\rm b$ には数字が入る「$\rm b-a^2$」って部分はまとめて数字だけの項にします。

以上を”平方完成”と言います。実際の問題で確認しましょう。

(1) は, $\rm x$ の係数が $\rm +2$ なんでその半分 $\rm (+1)$を使って $\rm (　　)^2$ の形を作ります。$\rm -7$ はそのままで, この（　　）を展開する出てくる余分な「$\rm 1$」を引いてあげる。最後に $\rm -7$ と $\rm -1$ をまとめて, $\textcolor{red}{\rm (x+1)^2-8}$

確認でもう１問だけ見ておきましょう。

(2) は, $\rm x$ の係数が $\rm -4$ なので､その半分の $\rm -2$ を使って $\rm (　　)^2$ の形を作る。展開するとここでも $\rm x^2-4x$ は上の式と同じ余分な「$\rm 4$」が出てきちゃうので, それを引いてあげる。最後に $\rm +2$ と $\rm -4$ をまとめてあげる。$\textcolor{red}{(x-2)^2-2}$

気付いた人もいるかもしれませんが, 緑で書いた部分は考えなくていいんです。余分なものとして登場する数字 $\rm 1$ とか $\rm 4$ は $\rm x$ の係数を半分にして２乗しただけ。その数を最後に引いてあげればいい。こんな流れで慣れちゃうと簡単です。早い人だと１問５秒ぐらいで終わっちゃいます。

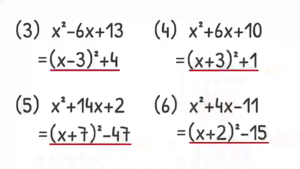残り(３)～(６)も練習してもらえれば良いかなと思います。解いた前提で話すと“答え”はこんな感じです。

よくある間違えとしては, 半分にした数字の２乗じゃなくて $\rm x$ の係数の２乗を引いちゃってるパターンとか, 引かずに足しちゃってるとか。そんなところですかね。

それでは, この「平方完成」を実際に“２次方程式”で使ってみましょう。

平方完成を使って解く２次方程式

大問２と大問３なんですが大問２は「穴埋め」が教科書通りの解き方で, 今の話と方法（考える順序）が違います。なので, 先に大問３を見ていきたいと思います。

さっきまでと違って「$\rm =$」のある方程式ですね。「平方完成」のやり方は同じで $\rm x$ の係数の”半分”の数字を使って２乗の形を作る。展開すると出てくる余分な $\rm 9$ を引いてあげる。$\textcolor{blue}{\rm (x-3)^2-12=0}$

ここからがさっきと違う部分になります。前回やった「平方根系」の解き方で２次方程式を解いていく。

まずは「$\rm (　　)^2=$」を作るため, $\rm -12$ を右辺に移項。$\textcolor{blue}{\rm (x-3)^2=12}$

形ができたら, 左はカッコと２乗をはずして, 右側は平方根を書く。

左に残った $\rm -3$ を右辺「$\rm ±$」の前に移項し, $\textcolor{blue}{\rm x=3±2\sqrt{3}}$

$\rm √$ の中は簡単な形に変形しないといけません。素因数分解して, $\textcolor{red}{\rm x=3±2\sqrt{3}}$

もう１問だけ。

まずは $\rm x$ の係数 $\rm 8$ の“半分”の数で２乗の形を作ってあげる。$\textcolor{blue}{\rm (x+4)^2-6=0}$

「$\rm (　　)^2=$」の形を作るので, $\rm -6$ を右辺に移項。$\textcolor{blue}{\rm (x+4)^2=6}$

左辺の「$\rm (　　)^2$」を外して, 右辺には平方根。$\textcolor{blue}{\rm (x+4)=±\sqrt{6}}$

左の $\rm +4$ を右辺に移項。よって, $\textcolor{red}{\rm x=-4±\sqrt{6}}$

続いて大問２。

ここは教科書通りの“穴埋”で, さっきまでのアプローチとちょっと手順が違います。意味は同じなんですけど, 混乱して解けないこともあるので, サラっとだけ見ておきます。

先ほどとは違い, きれいに「$\rm (　　)^2$」が作れるように, あらかじめ「両辺に余分な数を足しておく」方法です。

具体的に見ていくと, まずは「$\rm -3$」を右辺に移項。両辺に $\rm x$ の係数 $\rm 8$ の半分の $\rm 4$ を２乗した数, これを足してあげる。左辺を因数分解し, 右辺は定数項をまとめる。ここまで行くと“いつも通り”の平方根系の解き方になる。左辺は「$\rm (　　)^2$」を外して, 右辺は平方根を書く。最後は左に残った $\rm 4$ を移項して完成ですね。

今回は平方完成を使った解き方について行いました。

解説動画はコチラ ↓
<span data-mce-type="bookmark" style="display: inline-block; width: 0px; overflow: hidden; line-height: 0;" class="mce_SELRES_start"></span>