２次方程式の計算まとめ－２次方程式：中学３年生

今回は２次方程式の計算まとめについて行いたいと思います。

２次方程式の計算まとめ

大問７は２次方程式の計算のまとめ。

ここを全てクリアできたら, 理解が定着しているって感じでいいと思います。順番に見てくと, まずは「因数分解を使った解き方」ですね。

(1)は因数分解し終わってるので, それぞれの（　）が $\rm 0$ になる $\rm x$ の値を求めてあげる。左の（　）が $\rm 0$ になるのは $\rm x$ が $\rm 7$ のとき。右側が難しければ（　）の中身, $\rm 4x+3=0$ の方程式を作ってあげる。

(２)は１問目によく出るパターンですかね？こっちも因数分解系なんですけど「平方根を使う問題」との違い・特徴ってことで言うと, ～$\rm x$ があるってことですかね。因数分解だってなれば「$\rm =0$」を確認して, 左辺を因数分解。共通因数 $\rm x$ を前に出すタイプ。左の $\rm x$ が $\rm 0$ になるときと, 右の（　）が $\rm 0$ になるときの $\rm x$ の値。$\rm x=0,6$ が解になります。

続いても因数分解系ですね。

～$\rm x$ ってのがあるので, 左辺を因数分解してあげる。かけて $\rm -16$ 足して $\rm -15$ 数の組み合わせを考える。あとは同じで, 左右のカッコが $\rm 0$ になるときの $\rm x$ の値を求める。解は $\rm x=16,-1$ です。

(４)も左辺を因数分解。今回は $\rm (　　)^2$ の形なんで解が１つしかない珍しいタイプの問題ですね。解は $\rm x=3$ となります。

(５)はちょっとした応用ですかね。

ここも～$\rm x$ ってのがあるので, 「因数分解系」か「解の公式」。どちらにしても「$\rm =0$」を作るので, 右辺の $\rm 9$ を左に移項して $\rm 3$ で割ってあげる。簡単な式になるんで, あとは同じですよね。左辺を因数分解してあげて, 解は $\rm x=3,-1$ となります。

(６),(７)は平方根の考え方を使う問題２種類。

平方根系の問題は「$\rm x^2=$」って形を作らないといけませんでした。

(６)は左辺にある $\rm 2$ を移項すると「$\rm x^2=$」って形ができる。左側はカッコと２乗をはずして, 右側には平方根を書く。今回は $\rm 7$ の平方根なんで $\rm ± \sqrt{7}$。

(７)も基本的な流れは同じ。ここでは「$\rm x^2=$」ではなくて「$\rm (　　)^2=$」って形を作らないといけない。どちらにしてもまずは移項ですね。$\rm -7$ を移項して, カッコの前に付いてる数字で全体を割る。すると「$\rm (　　)^2=$」って形ができる。左辺はカッコと２乗を外して右辺には平方根を書く。ここは(６)とは違って, 最後に左に残った数字を右に持ってこないといけない。「$\rm ±$」の前に入れてあげて完成ですね

この問題は～$\rm x$ とかないんですけど因数分解系の２つ目の応用, 展開して移項するやつですね。複雑な形のものが出てくれば基本的にはコレか, 無理なら解の公式という流れになりますかね？

順番に見ていくと, まずは展開をする。「$\rm =0$」を作るために, 右にある項はすべて左辺に移項する。同類項をまとめ式を整理したら, あとはいつも通り左辺を因数分解。解は $\rm x=9,-3$ になります。

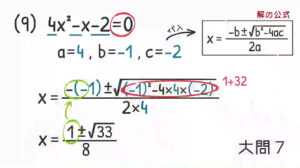最後は（９）解の公式ですね。

手順をおさらいすると「$\rm =0$」であるかをチェックして, $\rm a, b, c$ に入る値をメモして公式に代入する。今回みたいに「$\rm -$」が多いときは注意した方がいいですね。代入するときにカッコをつけて慎重に扱った方がいい。

√ の中を整理すると$\rm (-1)^2=1$ に $\rm -4×4×(-2)=32$ を加える。$\rm 1$ のところの符号も気をつけないとダメで「$\rm -$」が２つ並んでいるんで「$\rm +$」になりますかね。

これで計算問題を全て終えたので, 次回は「応用」,“２次方程式の利用”って範囲になります。パターン自体はないんで, ２回で完結するかなと思います。

今回は２次方程式の計算まとめについてでした。

解説動画はコチラ ↓
<span data-mce-type="bookmark" style="display: inline-block; width: 0px; overflow: hidden; line-height: 0;" class="mce_SELRES_start"></span>