正の数、負の数の加法のしかたについて成り立つ計算法則は次の $2$ つになります。
加法の交換法則 $\textcolor{blue}{a+b=b+a}$
加法の結合法則 $\textcolor{blue}{(a+b)+c=a+(b+c)}$
加法では上の法則が成り立つので、$3$ つ以上の数を加えるときには、数の順序や組み合わせを変えて、どの $2$ 数から計算しても同じ結果になります。
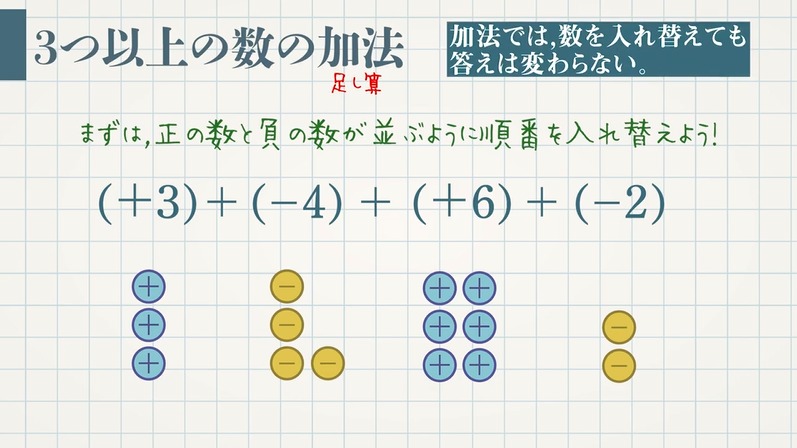
それでは、$(+3)+(-4)+(+6)+(-2)$ を法則を使って計算してみましょう。
正の数、負の数の加法のしかたについて成り立つ計算法則は次の $2$ つになります。
加法の交換法則 $\textcolor{blue}{a+b=b+a}$
加法の結合法則 $\textcolor{blue}{(a+b)+c=a+(b+c)}$
加法では上の法則が成り立つので、$3$ つ以上の数を加えるときには、数の順序や組み合わせを変えて、どの $2$ 数から計算しても同じ結果になります。
それでは、$(+3)+(-4)+(+6)+(-2)$ を法則を使って計算してみましょう。

【例題】次の計算をしなさい。
$\textcolor{green}{(+3)+(-4)+(+6)+(-2)}$
まずは正の数と負の数が並ぶように順序を入れかえます。加法の交換法則 $\textcolor{blue}{a+b=b+a}$
$(+3)+(-4)+(+6)+(-2)$
$= (+3)+(\textcolor{blue}{+6})+(\textcolor{blue}{-4})+(-2)$
次に、組み合わせを変えて正の数と負の数をまとめます。加法の結合法則 $\textcolor{blue}{(a+b)+c=a+(b+c)}$
$(+3)+(\textcolor{blue}{+6})+(\textcolor{blue}{-4})+(-2)$
$=\{(+3)+(+6)\}+\{(-4)+(-2)\}$
$=(+9)+(-6)$
$=\textcolor{red}{+3}$
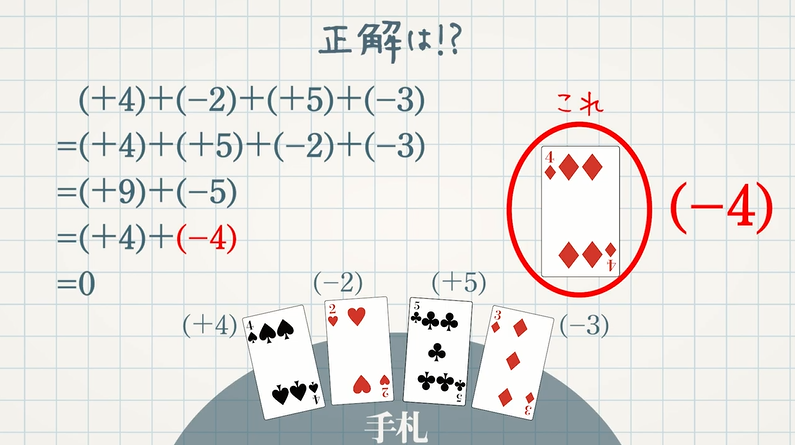
【問題】黒(♠・♣)のカードが正の数、赤(♦・♥)のカードが負の数であるとき、手札の合計を「$\textcolor{green}{0}$」にするには、「♠の$\textcolor{green}{5}$ , ♥の $\textcolor{green}{3}$ , ♣の $\textcolor{green}{2}$ , ♦の $\textcolor{green}{4}$」のうち、どのカードを引けば良いか答えなさい。
今、手札 $4$ 枚の合計は、
$(+4)+(-2)+(+5)+(-3)$
$=(+4)+(+5)+(-2)+(-3)$
$=\{(+4)+(+5)\}+\{(-2)+(-3)\}$
$=(+9)+(-5)=\textcolor{blue}{+4}$
手札の合計を $\textcolor{blue}{0}$ にしたいので、$\textcolor{blue}{-4}$ を足せば、$(+4)+(-4)=0$ となる。よって、答えは ♦の4
コンテンツやシステムに関するお問い合わせ・オファーはこちらから