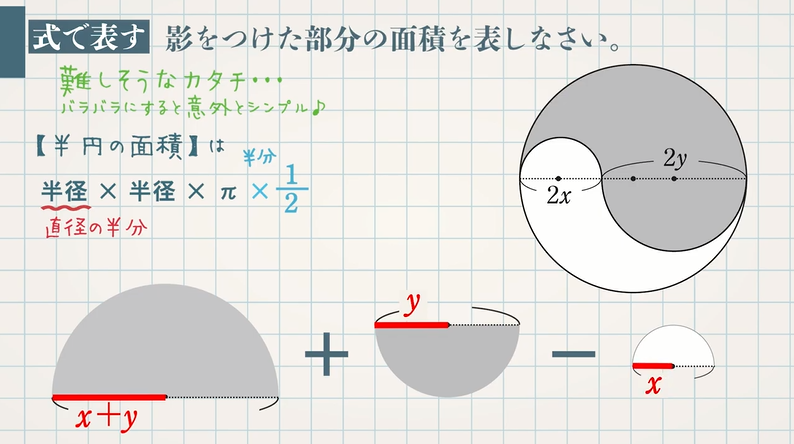
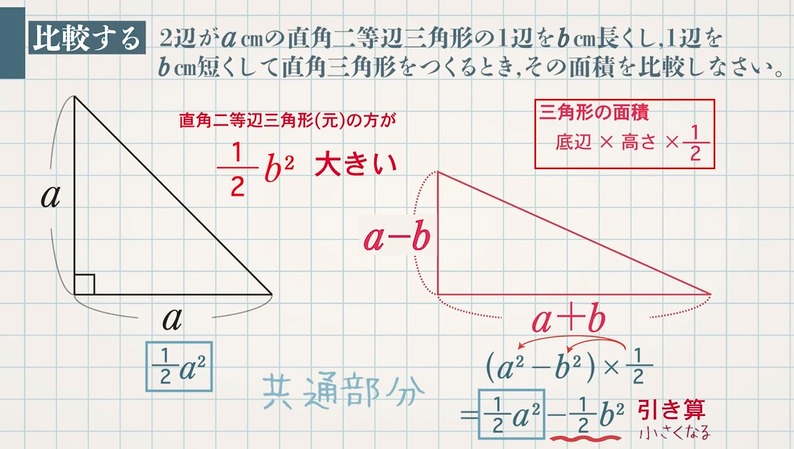
式の計算を利用して、図形の性質を証明する問題として代表的なものは $\textcolor{blue}{{\rm S}=aℓ}$ の証明ですが、その他にも頻出問題がいくつかあります。

【問題】L字型の図形と面積が等しい正方形の $\textcolor{green}{1}$ 辺の長さを求めなさい。

青の長方形の面積は $9×4=\textcolor{blue}{36}$ 

緑の長方形の横の長さは $x+8$ 、縦の長さは $x+5-9=x-4 $ となります。よって、その面積は $(x+8)(x-4)=\textcolor{blue}{x^2+4x-32}$ 

青、緑の面積の合計は、

\begin{eqnarray} &　&36+x^2+4x-32\\ &=&x^2+4x+4　因数分解\\ &=&\textcolor{blue}{(x+2)^2} \end{eqnarray}

よって、正方形の $1$ 辺の長さは $\textcolor{red}{(x+2)}$ となる。

【問題】影をつけた部分の面積を表しなさい。

影のつけた部分の面積は、図の通り半径 $\textcolor{blue}{x+y}$ と 半径 $\textcolor{blue}{y}$ のグレーの半円の和から半径 $\textcolor{blue}{x}$ の白の半円をひけば求めることができます。

\begin{eqnarray} &　&(x+y)^2\textcolor{blue}{×π×\frac{1}{2}}+y^2\textcolor{blue}{×π×\frac{1}{2}}-x^2\textcolor{blue}{×π×\frac{1}{2}}　\\\\ &=&\{(x+y)^2+y^2-x^2\}\textcolor{blue}{×π×\frac{1}{2}}\\\\ &=&(2xy+2y^2)×π×\frac{1}{2}\\\\ &=&\textcolor{red}{πy(x+y)} \end{eqnarray}

【問題】 $\textcolor{green}{2}$ 辺が $\textcolor{green}{a\rm cm}$ の直角二等辺三角形の $\textcolor{green}{1}$ 辺を $\textcolor{green}{b \rm cm}$  長くし、$\textcolor{green}{1}$ 辺を $\textcolor{green}{b\rm cm}$ 短くして直角三角形をつくるとき、その面積を比較しなさい。

もとの直角二等辺三角形の面積は、 $a×a×\frac{1}{2}=\textcolor{blue}{\frac{1}{2}a^2}$

変更後の三角形の面積は、

$(a+b)(a-b)×\frac{1}{2}=(a^2-b^2)×\frac{1}{2}=\textcolor{blue}{\frac{1}{2}a^2-\frac{1}{2}b^2}$

$\textcolor{blue}{\frac{1}{2}a^2}$ が共通部分なので、もとの直角二等辺三角形の方が $\textcolor{red}{\frac{1}{2}b^2}$ 大きい