因数分解を使う解き方－２次方程式：中学３年生

本日は「２次方程式」の計算の中でも「因数分解を使う解き方」についてみていきたいと思います。まずは２次方程式の概要から確認していきましょう。

２次方程式の概要

$\rm ax²+bx+c=0(a≠0)$ という式を“２次方程式”と言います。$\rm a,b,c$ にはそれぞれ数字が入りますが, $\rm a$ は $\rm 0$ じゃありません。

「$\rm x$」は, 今までの方程式・連立方程式と同じく“解”といい, $\rm x$ の値を求める（計算する）ことを“２次方程式を解く”といいます。

２次方程式の解き方にはバリエーションがなく, ３年生の初めに習った「因数分解」を使う方法と, 「平方根の考え」を使う方法の２種類しかありません。ここまで習った範囲の“総復習”と言えます。なので, この２つの単元が「ちょっと怪しいぞ」って人は復習してからチャレンジする方が無難かと思います。

因数分解を使った解き方：基本

因数分解を利用して解く方法のポイントは必ず「$\rm =0$」という形をつくることです。

(１)は元々「$\rm =0$」の形になっています。左辺が因数分解できるので, かけて $\rm 6$ , 足して $\rm -5$ になる２つの数字を考える。

$\rm (x-3)(x-2)=0$ となります。

方程式なので, $\rm (x-3)×(x-2)$ が「$\rm 0$」になるときの「$\rm x$」の値を求めないといけません。左の $\rm (x-3)$ が $\rm 0$ になるときの $3$ 。右の $\rm (x-2)$ が $\rm 0$ になるときの $2$ 。

$\rm x=3, 2$ がこの方程式の解になります。

２次方程式の解は基本的に“２つ”ですので, しっかり覚えておきましょう。

解き方はさっきと同様で, かけて $\rm -24$ , 足して $\rm 5$ になる２つの数字を考える。

$\rm (a+8)(a-3)=0$ になります。

それぞれ $\rm 0$ にするためには $\rm -8$, $\rm 3$ を入れればいいので, 解は $\rm a=-8, 3$。間違って $\rm x=$ としないように注意しましょう。

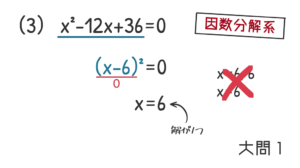ここも左辺を因数分解すると, $\rm (x-6)^2$ となります。この式を $\rm 0$ にする $\rm x$ の値は, $\rm x=6$ しかありません。これは２次方程式の中では“解が１つしかない”特殊な部類になります。$\rm x=6,6$ のように, ２つ書いて失点しないようにしましょう。

この問題は共通因数を前に出すパターンの因数分解になります。共通因数 $\rm x$ を前に出して, 残りをカッコの中に書きます。分配の逆になる因数分解ですね。

カッコだけ見て, $\rm x=4$ で終わらないようにしましょう。カッコの前にある $\rm x$ が $\rm 0$ になるとき, $\rm x=0$ も解になるので, 忘れないように注意が必要です。

(5)は $\rm A^2-B^2$ の形なので, 因数分解すると $\rm (x+7)(x-7)$ となります。ここも左側を $\rm 0$ にする $\rm -7$ と右側を $\rm 0$ にする $\rm 7$ でOKです。

すでに平方根の範囲で「$\rm ±$」の書き方を習っているので, $\rm ±7$ と書いても大丈夫です。

この式は, 因数分解をした後だと思ってください。右のカッコが $\rm 0$ になるときの $\rm -1$ は答えられる人が多いのですが, 左のカッコを $\rm 0$ にする $\rm x$ の値はどうでしょうか？

暗算で解くのが難しい人は, 式を作ればOKです。$\rm 2x-3=0$。 $\rm -3$ を右辺に移行をして $\rm 2$ で割る。整数にならないので分数ですね。文字の係数が分母にきます。

因数分解を使った解き方：応用

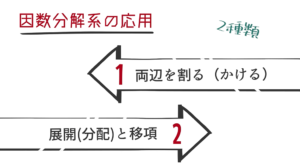
因数分解を使った解き方の応用は, 「１. 両辺を割ったり・かけたりするもの」「２．展開して移項するもの」この２パターンしかないです。それぞれ確認していきましょう。

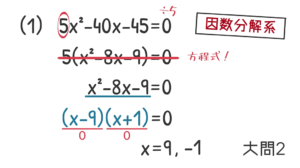まず「１. 両辺を割ったり・かけたりするもの」。

共通因数「$\rm 5$」でくくれば因数分解できなくはないですが, 今回は方程式。等式（イコールのある式）なので, すべての数字を $\rm 5$ で割りましょう。そうすると, 大問１で解いた問題と同じ形になります。

あとは今まで通り, 左辺を因数分解して“左”が $\rm 0$ になる $\rm x$ の値。“右”が $\rm 0$ になる $\rm x$ の値を求める。解は, $\rm x=9,-1$ になります

(2)は分数ですね。

分母の最小公倍数（今回でいうと $\rm 6$ ）を全体にかけてあげる。分数が外れて簡単な式になった左辺を因数分解。解は, $\rm x=3,-1$ になります。

先頭に「$\rm -$」がきてるので, 全体に $\rm -1 $ をかけましょう。先頭の「$\rm -$」をなくしてから, 因数分解ですね。気をつけないといけないのは, すべての符号（プラス・マイナス）が入れ替わるということ。$\rm +6$ は $\rm -6$ , $\rm -8$ は $\rm +8$ に変えてあげないといけないですね。

あとは同じで, 左辺を因数分解。解は, $\rm x=2,4$ になります。

大問３は「２．展開して移項するもの」。

このパターンの問題は, 式の中に分配 or 展開できるものがあり, 「$\rm =0$」ではありません。なので, まずは「分配・展開をする」。それが終われば右辺（右側）にある全ての項を左側に移項し, 同類項をまとめましょう。

大問１と同じような簡単な式ができるので, 今まで通り因数分解。解は, $\rm x=3,2$ になります。

もう１,２問だけ確認しておきましょう。

まずは, 左辺を展開。乗法公式で解きましょう。４回かけて同類項をまとめることも出来なくはないですが, スピード的に限界があるので公式を使いましょう。

右辺にある $\rm 5$ を左辺に移項し, 整理して因数分解。解は, $\rm x=8,2$ になります。

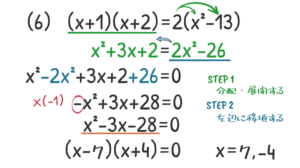最後に応用形２つの複合問題をみておきましょう。

左辺は展開・右辺は分配します。そして, 右辺にある $\rm 2x^2-26$ を左辺に移項し, 式を整理します。

$\rm x^2$ の前に「$\rm -$」があるので, 全体に「$\rm -1$」をかけて式を変形します。符号には注意しましょう。

式が整理できたら因数分解。解は, $\rm x=7,-4$ になります。

以上が因数分解系の問題になります。

解説動画はコチラ ↓
<span data-mce-type="bookmark" style="display: inline-block; width: 0px; overflow: hidden; line-height: 0;" class="mce_SELRES_start"></span>