解の公式を使った解き方－２次方程式：中学３年生

今回は解の公式を使った解き方について行いたいと思います。それではみていきましょう。

解の公式

今までやってきた２次方程式の計算問題は全部「解の公式」で解けるんですが, この公式はとても“面倒くさい”し, 間違えやすい。なので, 他の解き方でいけるなら, そっちで解いた方が良いんですね。

「因数分解系」とか「平方根系」で解けない, ややこしい“平方完成”をしないといけない問題が必ず数問は出題されますが, そこを落とさないようにする為, この公式を利用するイメージです。

公式は, $\textcolor{red}{\rm x=\frac{-b±\sqrt{b^2-4ac}}{2a}}$。これが大問 $\rm 4$ の答えになります。

ここは“きっちり”覚えてほしい。自分で作れる人は覚えなくて良いんですけど「$\rm +$」か「$\rm -$」の違いでも“答え”変わっちゃうんで, ちゃんと覚えないと意味がありません。

続いて大問５。

前提の話をすると, 公式の $\rm a, b, c$ ってのはそれぞれ $\rm x^2, x$ の係数と定数項になります。

なので(１)だと, 見たまま数字を答えればいい。ただ１点注意が必要なのは「$\rm =0$」にしないといけない。なんで, (２)だとまずは右辺の$\rm -4$ を左に移項して「$\rm =0$」を作ってあげる。今回 $\rm a$ に数字ないんですけど $\rm 1$ の省略なんで $\rm -1$ ですね。$\rm b$ が $\rm -9$, $\rm c$ が $\rm 12$。

ここは“要注意”ですね。

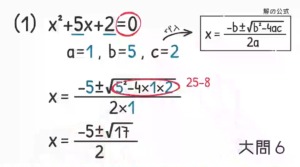実際の使い方を見ていくと, まずは「$\rm =0$」であることを確認して$\rm a, b, c$ の数字をメモっておく。あとは「解の公式」に $\rm a, b, c$ の値を代入するだけですね。

気をつけないといけないのは $\rm √$ の中の計算。今回だと$\rm 5^2=25$ から $\rm 4×1×2=8$ を引くって感じですかね。整理して答え $\textcolor{red}{\rm x=\frac{-5±\sqrt{17}}{2}}$

中学分野では $\rm √$ の中は「$\rm -$」になることはないので, もしなったら“計算ミス”。多分, $\rm -4ac$ のところの符号が間違ってるパターンだと思うので, チェックが必要ですかね。

あと２問ほど確認しましょう。

ここもさっきと同じで「$\rm =0$」を確認して, $\rm a, b, c$ の値をメモする。

公式に代入すると, $\textcolor{blue}{\rm x=\frac{-10±\sqrt{128}}{2}}$

$\rm √$ の変形ができる場合はしてあげないといけない。

$\rm √$ の外に数字を出すことで, 今回は約分ができるようになります。

$\rm 2$ と $\rm -10$ と $\rm 8$ を $\rm 2$ で割ってあげる。

よって, $\textcolor{red}{\rm -5±4\sqrt{2}}$

ここも手順は同じですかね「$\rm =0$」かチェックして $\rm a, b, c$ の値をメモって代入。

$\rm √$ の中を整理すると,「$\rm 4^2$」になるので $\rm √$ が外れる。ここも全ての数 $\rm (8, 4, 6)$ が $\rm 2$ で割れる。約分をすると分子の　$\rm -4$ と $\rm ±2$ は計算できるので計算しないといけない。$\rm -4+2=-2$。もう一方は, $\rm -4-2=-6$。ここも約分して最終の答えです。

今回は解の公式を使った解き方についてでした。

解説動画はコチラ ↓
<span data-mce-type="bookmark" style="display: inline-block; width: 0px; overflow: hidden; line-height: 0;" class="mce_SELRES_start"></span>